1 : даны прямая и три точки а, в, c, не лежащие на этой прямой. известно, что отрезок ав пересекает прямую, а отрезок ас не пересекает её. пересекает ли прямую отрезок вс? объясните ответ.
2 : даны прямая и четыре точки а, в, с и d, не лежащие на этой прямой. пересекает ли прямую отрезок ad, если: 1) отрезки ав, вс и cd пересекают прямую; 2) отрезки ас и вс пересекают прямую, а отрезок bd не пересекает; 3) отрезки ав и сd пересекают прямую, а отрезок вс не пересекает; 4) отрезки ав и cd не пересекают прямую, а отрезок вс пересекает; 5) отрезки ав, вс, сd не пересекают прямую; 6) отрезки ас, вс и bd пересекают прямую? объясните ответ.
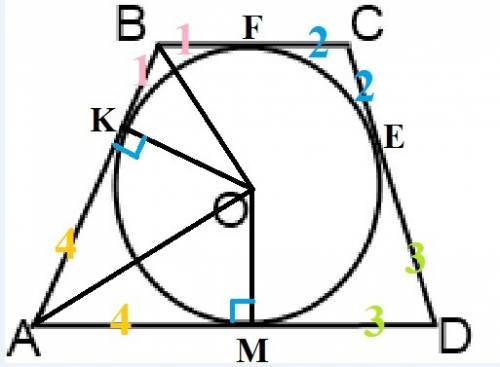
Проведём из т.С прямую СМ║ВД (точка М - точка пересечения СМ и АД)
ВСМД - параллелограмм ⇒ ВС=ДМ=3 , ВД=СМ=4 .
Так как средн. линия = 2,5 , то 2,5=(АД+ВС):2 ⇒ АД+ВС=2·2,5=5
АМ=АД+ДМ=АД+ВС=5
ΔАСМ имеет площадь ,равную площади трапеции, так как
S(трапеции)=(АВ+ВС)/2 ·h = 1/2·AM·h (h - высота трапеции СН)
S(ΔАСМ)=1/2·АМ·h (h - высота ΔАСМ = высоте трапеции СН)
Найдём площадь ΔАСМ, заметив, что он прямоугольный, так как
АМ=5, а √(АС²+СМ²)=√(3²+4²)=√25=5, то есть выполняются условия теоремы Пифагора: АМ²=АС²+СМ² .
S(ΔАСМ)=1/2·АС·СМ=1/2·3·4=6 ⇒ S(АВСД)=6
P.S. Если бы ΔАСМ не оказался прямоугольным, то его площадь можно было бы найти по формуле Герона, т.к. все его стороны оказались известными.