Бисектриса прямого угла прямоугольного треугольника делит гіпотенузу на отрезки 40 см и 30 см. Найдите периметр треугольника.
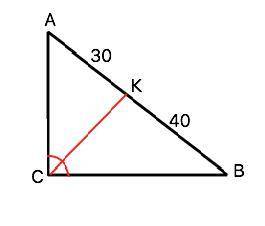
Обозначим треугольник АВС; СК - биссектриса. АК=30 см, ВК=40 см.
Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон. (свойство). АК:ВК=30:40=3:4. =>
АС:ВС=3:4. Из отношения катетов видно, что треугольник АВС - так называемый «египетский» с отношением сторон 3:4:5. .
Примем коэффициент отношения равным а.
Тогда АС=3а, ВС=4а, гипотенуза АВ=5а.
АВ=АВ+ВК=30+40=70 (см) => а=70:5=14(см).
Р=3а+4а+5а=12а
Р=12•14=168 (см)
диагональ делит прямоугольник на два равных прямоугольных треугольника. по условию, стороны прямоугольника (а значит, катеты каждого из прямоугольных треугольников) относятся как 16/10=8/5.
обозначим стороны прямоугольника (т.е. катеты треугольников) как 8х - большая и 5х - меньшая. по теореме пифагора в прямоугольном треугольнике(стороны прямоугольника - катеты, диагональ - гипотенуза) получим:
(8х)"+(5х)"=140" (" означает возведение в квадрат)
64х"+25х"=19600
89х"=19600
х=140/? 89 (? - квадратный корень)
стороны соответственно равны:
8*140/? 89=1120/? 89
5*140/? 89=700/? 89
ответ: стороны равны 1120/? 89 и 700/? 89 (можно избавиться от иррациональности в знаменателе, тогда получим: 1120*? 89/89 и 700*? 89/89)
(есть второй решения через тангенс угла в этом же прямоугольном треугольнике, но по-моему, этот проще).
p [1 ;-5;3] x=1; y=-5; z=3
k[-3;0;8] x=-3; y=0; z=8
m[2;3;-3] x=2; y=3; z=-3
С каждой координатой выполняется действие как в векторе 3p-3k+4m
X = 3*1 - 3*(-3) + 4*2 = 20
Y = 3*(-5) - 3*0 + 4*3 = -3
Z = 3*3 - 3*8 + 4*(-3) = -27
3p-3k+4m [20; -3; -27]