ответ: а) 16√3 см²; б) 4√3 см²
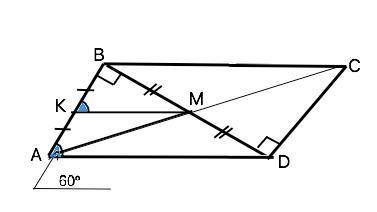
Объяснение:Диагональ BD перпендикулярна АВ ( дано), СD||АВ ⇒ BD перпендикулярна CD и делит АВСD- на два равных прямоугольных треугольника.
КМ||АD, М - середина ВD ⇒ КМ - средняя линия ∆ АВD, поэтому АD=2КМ=8 см.
Угол А=60°, ⇒ АВ=АD•cos60°=4 (см)
Площадь параллелограмма по одной из формул равна произведению соседних сторон на синус угла между ними:
Ѕ(АВСD)=4•8•√3/2=16√3 (см²)
Т.к ∆ ( АВD)=∆ DCВ, а т.М = середина ВD, отрезок АМ - медиана ∆ АВD и делит его на два равновеликих треугольника. =>
Ѕ(AMD)=S(ABCD):4=16√3:4=4√3см²
Опустим из т.А перпендикуляр АН на плоскость второй грани. Прямая, перпендикулярная плоскости, перпендикулярна любой прямой, лежащей в ней.
АН⊥НD. НD- проекция наклонной АD. По т. о 3-х перпендикулярах HD⊥DC, и АD⊥DC,⇒ угол АDH-равен углу данного двугранного угла, т.е. 60°.. Треугольник АНD – прямоугольный по построению. DН=АD•cos60°=7,5 см. АН=АD•sin60°=7,5√3 см. Проведем НК║DC. HD и ВС перпендикулярны CD. Четырехугольник ВСDH - прямоугольник, КС=HD=7,5 см. ⇒ ВК=ВС-КС=0,5 см. ∆ НКВ - прямоугольный ( угол К=90°). По т.Пифагора ВН²=HK²+BK²=84²+0,5²=7056.25. Так.как АН⊥ВН, из прямоугольного ∆ АНВ по т.Пифагора АВ=√(BH²+AH²)=√(7056.25+168,75)=85 см