Доказательство утверждения проводится следующим образом. Сначала принимают предположение, что утверждение неверно, а затем доказывают, что при таком предположении было бы верно некоторое утверждение , которое заведомо неверно. Полученное противоречие показывает, что исходное предположение было неверным, и поэтому верно утверждение , которое позакону двойного отрицания равносильно утверждению .
В интуиционистской логике закон исключённого третьего не действует, поэтому такие доказательства в ней не принимаются.
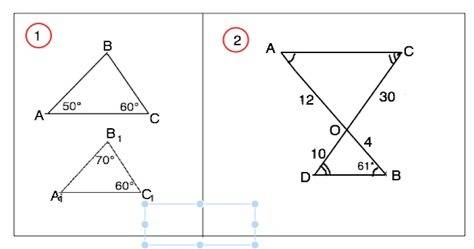
1) Сумма углов треугольника 180°. В ∆ АВС угол В=180°-50°-60°=70°. В ∆ А1В1С1 угол А1=180°-708-608=50°. Треугольники АВС и А1В1С1 подобны по равенству всех углов.
2) По условию АС║BD, АВ и СD - секущие. Образовавшиеся при пересечении секущими параллельных прямых накрестлежащие углы равны. ⇒ ∠СAО=∠DBO=61°. Треугольники АОС и BOD подобны по равенству накрестлежащих углов, а стороны, содержащие вертикальные углы при О - пропорциональны. k=АО:ВО=12:4=3, k=СО:DO=30:10=3. Отношение площадей подобных фигур равно квадрату коэффициента их подобия. S(AOC):S(BOD)=k²=3²=9
Если коэффициент пропорциональности х, то меньший угол 2х, а больший 3х. Их сумма 2х+3х=90, откуда х=90/5; х= 18, значит, больший угол равен 18°*3=54°
ответ 54°
2. Т.к. АС=ВС, то по определению равнобедренного треугольника ΔАВС равнобедренный с основанием АВ, тогда углы при основании АВ равны, угол В равен 40°, а угол С равен 180°-(∠А+∠В)=180°-(40°+40°)=100°
ответ 100°
3. Углы А и В в ΔАВС равны по свойству углов при основании в равнобедренном треугольнике. Поэтому угол А равен
(180град. -120град.)/2=30 град.
ответ 30 градусов