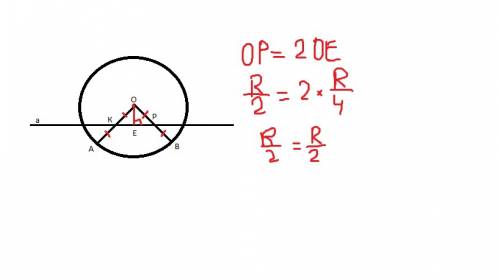
Обозначим буквами вершины треугольника АВС (начиная с нижней левой вершины), а точку пересечения прямой (показан голубым цветом) со стороной АС за К.
Объяснение:
Сначала мы должны опустить высоту ВН в треугольнике АВС, которая также является высотами треугольников АВК и ВКС.
1) Высота в равнобедренном треугольнике является медианой и биссектрисой
следовательно ->
-> АН=НС=(21+11)÷2=16
2) Рассмотрим треугольник ВНК:
НК=НС-КС=16-11=5
По т. Пифагора:
ВН^2=169-25
ВН=12
3)Можно рассмотреть любой из треугольников АВН и ВНС
По т. Пифагора:
х^2=144+256
х^2=400
х=20
ОТВЕТ: х=20
Всего лишь надой найти площадь равнобедренного треугольника, если дан угол при основании и расстояние от вершины основания до центра вписанной окружности.
β - угол при основании
L расстояние от вершины основания до центра вписанной окружности
Радиус вписанной окружности
r = L*sin(β/2)
половинка основания
a/2 = L*cos(β/2)
Половина угла при вершине
(180-2β)/2 = 90 - β
Эта же половинка основания, но в треугольнике, равном половине большого
a/2 = b*sin(90-β)
a/2 = b*cos(β)
b = a/(2*cos(β)) = 2L*sin(β/2)/(2*cos(β)) = L*cos(β/2)/cos(β)
полупериметр
p = b + a/2 = L*cos(β/2)/cos(β) + L*cos(β/2) = L*cos(β/2)*(1+1/cos(β))
и площадь через полупериметр и радиус вписанной окружности
S = rp = L*sin(β/2)*L*cos(β/2)*(1+1/cos(β)) = 1/2*L²*sin(β)*(1+1/cos(β))
и всего таких треугольника 4
S₄ = 4*S =2*L²*sin(β)*(1+1/cos(β))