
Задание №1
Объяснение:
Пирамида SABCD. Апофема SH - высота треугольника SAB. O - точка пересечения диагоналей основания, SO - высота пирамиды.
1) Рассмотрим прямоугольный треугольник OHS. По теореме пифагора:
OH² = SH² - SO²
OH² = 4a² - 3a²
OH = a
По теореме Фалеса: BC = 2OH = 2a
Сторона основания 2a
2) SHO - линейный угол двугранного угла SABO. Найдя его, найдем и SABO, следовательно угол между боковой гранью и основанием.
Из прямоугольного треугольника SHO:
sin<SHO = SO/SH
sin<SHO = a√3/2a = √3/2
<SHO = 60°
Угол между боковой гранью и основанием 60°
3) S = Sбок + Sосн
В основании квадрат, значит Sосн = AB² = (2a)² = 4a²
Sбок = Pосн*SH/2
Pосн = 4*2a = 8a
Sбок = 8a*2a/2 = 8a²
S = 8a² + 4a² = 12a²
Площадь 12а²
4) Из точки О (это и есть центр основания) проводим перпендикуляр к апофеме SH, обозначаем H1. SH1 - расстояние от центра основания до плоскости боковой грани.
Из прямоугольного треугольника OH1H:
sin<SHO = OH1/OH
но sin<SHO = √3/2
√3/2 = OH1/a
OH1 = a√3/2
ответы: a; 60°; 12а²; a√3/2
2 )Строишь отрезок любой из заданных величин.Затем из концов отрезка строишь окружности , радиусы которых равны двум оставшимся.Точка пересечения этих окружностей будет третей вершиной.Соедини точку с концами отрезка и получишь искомый треугольник.
3) Побудова:
а) будуємо відрізок АВ = 6 см;
б) з обох його кінців А і В як з центрів проводимо кола, радіуси яких дорівнюють АС = 5 см і ВС = 4 см;
в) сполучаємо точки АіВ відрізка АВ з однією із точок С перетину кіл. Трикутника ABC - шуканий.
2) Побудова:
а) будуємо відрізок АВ - 2 см;
б) з обох його кінців А і В як з центрів проводимо кола, радіуси яких дорівнюють АС = ВС = 2 см;
в) сполучаємо точки АіВ відрізка АВ з однією із точок С перетину кіл. Трикутник ABC - шуканий.
а 1 я не знаю(
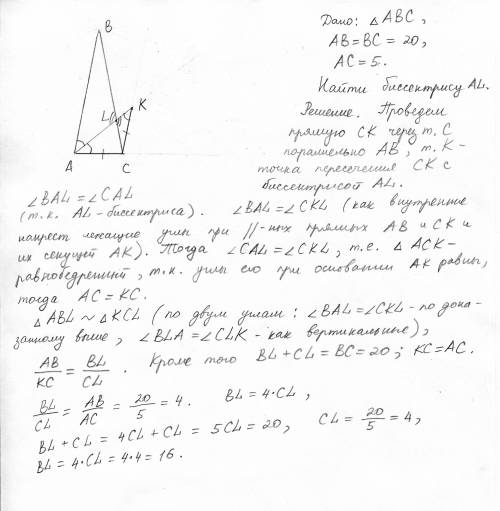
Объяснение:
Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам:
a/b=x/y
a=20 см
b=5 см
у=20-x
20/5=х/(20-х)
4(20-х)=х
80-4х=х
5х=80
х=16 (см)
y=20-х=20-16=4 (см)
Длина биссектрисы выисляется по фомруле:
(см)
ответ: длина биссектрисы 6 см.