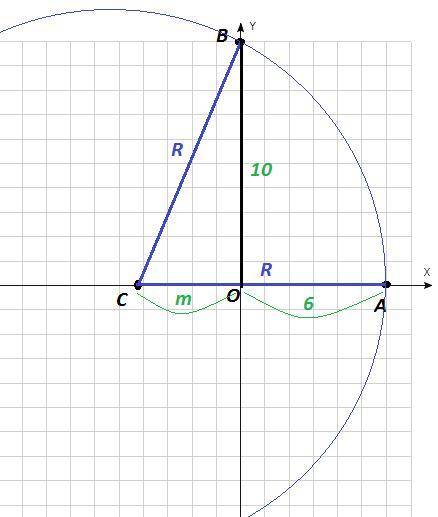
Координаты точки на оси Ox : A (6;0)
Координаты точки на оси Oy : B (0;10)
Так как 6<10, значит, центр окружности лежит слева от оси Oy.
Координаты центра окружности на оси Ox : С(-m;0)
R = CA = m + 6
ΔBOC , R = CB, теорема Пифагора :
R² = m² + 10²
(m + 6)² = m² + 10²
m² + 12m + 36 = m² + 100
12m = 64; 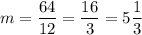
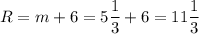
Общее уравнение окружности с центром в точке С и радиусом R
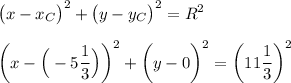
Так как абсцисса центра окружности отрицательная, то в первой скобке должен быть знак плюс.
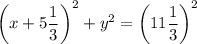
Если подгонять ответ под схему в условии, то знак минус придётся убрать в числитель дроби :
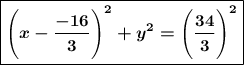
1), 2), 6), 8).
Объяснение:
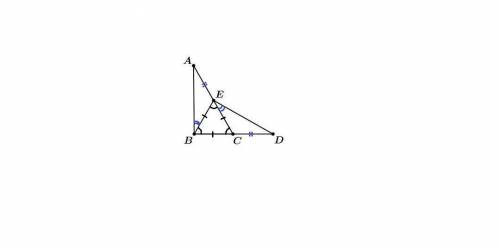
ΔАВС = ΔDEB,
АВ = DE, АС = DB, значит ВС = ВЕ, т.е. ΔВЕС равнобедренный
В равных треугольниках против равных сторон лежат равные углы, значит
∠DBE = ∠ACB, тогда
ΔВЕС равнобедренный с основанием ВС.
Итак, ВЕ = ЕС = ВС, т.е. ΔВЕС равносторонний.
∠АВЕ = ∠АВС - ∠ЕВС
∠DEC = ∠DEB - ∠BEC
∠АВС = ∠DEB из равенства треугольников,
∠EBC = ∠BEC, как углы равностороннего треугольника, значит
∠АВЕ = ∠DEC.
АЕ = АС - ЕС
CD = DB - BC
AC = DB по условию,
ЕС = ВС, так как ΔВЕС равносторонний, значит
АЕ = CD.
1) Треугольник BCE равнобедренный - верно.
2) Треугольник BCE равносторонний - верно.
3) ∠ABC = 90° - нельзя утверждать.
4) Треугольник ECD равнобедренный - нельзя утверждать.
5) AE = BC - нельзя утверждать.
6) AE = CD - верно.
7) ∠ABE = ∠CDE - нельзя утверждать.
8) ∠ABE = ∠CED - верно.