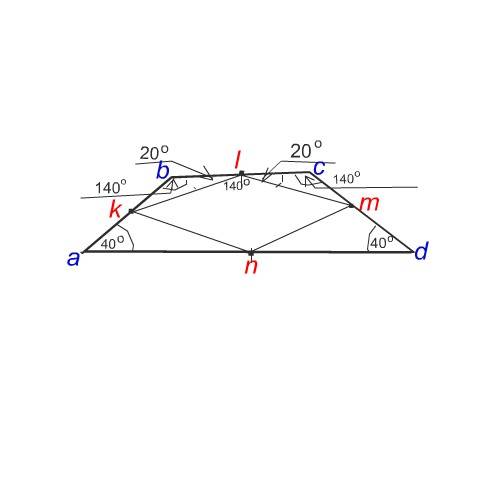
При решении следует учитывать. что трапеция не только равнобедренная, но что и меньшее основание трапеции длиной равно боковым сторонам.
Сделаем рисунок.
Δ kbl равнобедренный, так как kb=bl как половины равных сторон аb и bс
Тупой угол b трапеции равен 180°-40°=140° .
Поэтому сумма углов bkl и blk равна 180°-140°=40°, а каждый из них равен 20° .
Углы треугольника lcm равны по величине углам треугольника bkl, так как сами эти треугольники равны.
Отсюда величина угла klm, большего в четырехугольнике klmn, равна 180°-40°=140°
Равные углы отмечены равным количеством "скобок"
∠А = ∠А₁ (углы помечены одной скобкой)
∠В = ∠В₁ (углы помечены тремя скобками)
∠С = ∠С₁ (углы помечены двумя скобками)
Равные стороны помечены равным количеством "чёрточек"
АС = А₁С₁ (одна черточка)
ВС = В₁С₁ (две черточки)
АВ = А₁В₁ (три черточки)