1. Расстояние от центра окружности до точки, из которой проведены две касательные, делит угол A пополам. Значит угол HAO равен 30 градусам. Проведем радиус от точки O в точку касания окружности с касательной. Радиус, проведенный из центра окружности к точке касания является перпендикуляром к касательной. Получается прямоугольный треугольник HAO. В прямоугольном треугольнике катет, лежащий против угла в 30 градусов половине гипотенузы. OA - гипотенуза
OH=1/2*6
OH=3
OH-радиус окружности
ответ:R=3
2.28 градусов
3.7
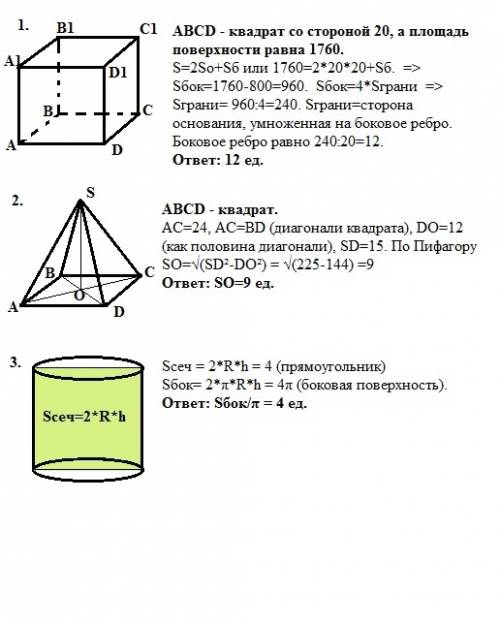
1. ABCD - квадрат со стороной 20, а площадь поверхности призмы равна 1760. Sп=2So+Sб или 1760=2*20*20+Sб. => Sбок=1760-800=960. Sбок=4*Sграни => Sграни= 960:4=240. Sграни=сторона основания, умноженная на боковое ребро. Боковое ребро равно 240:20=12.
ответ: 12 ед.
2. ABCD - квадрат. АС=24, АС=BD (диагонали квадрата), DO=12 (как половина диагонали), SD=15. По Пифагору SO=√(SD²-DO²)=√(225-144) =√81 = 9 ед.
ответ: SO=9 ед.
3. Sсеч = 2*R*h = 4 (прямоугольник). Sбок= 2*π*R*h = 4π (боковая поверхность).
ответ: Sбок/π = 4 ед.
y = 0
3x-4*0+1=0
3x = -1
x = -1/3
(-1/3;0)
2. С оосью Y
x = 0
3*0-4y+1 = 0
4y = 1
y =1/4
(0;1/4)