
Построение:
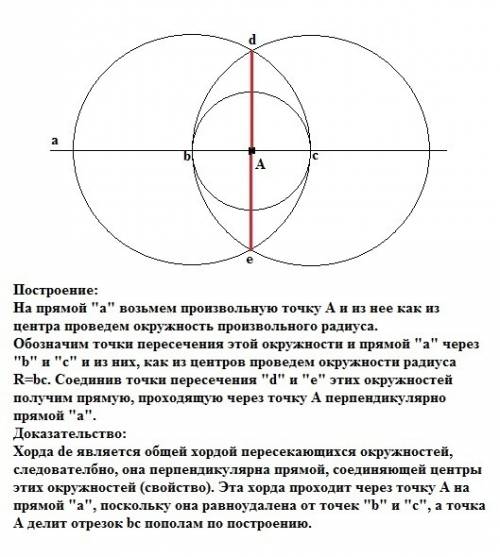
На прямой "а" возьмем произвольную точку А и из нее как из центра проведем окружность произвольного радиуса. Обозначим точку пересечения этой окружности с прямой "а" через "b" и "с" и из них, как из центров проведем окружности радиуса R=bс. Соединив точку пересечения "d" и "е" этих окружностей получим прямую, проходящую через точку А перпендикулярно прямой "а".
Доказательство:
Хорда de является общей хордой пересекающихся окружностей, следовательно, она перпендикулярна прямой, соединяющей центры этих окружностей (свойство). Эта хорда проходит через точку А на прямой "а", поскольку она равноудалена от точек "b" и "с", а точка А делит отрезок bс пополам по построению.
c^2=a^2+b^2
c^2=16+25
c^2=41
c= √41