ответ:√137 (ед. длины)
Объяснение:
Площадь треугольника равна половине произведения высоты на сторону, к которой проведена. Тогда: Ѕ=а•h:2 ⇒ a•h=2S
Высота тупоугольного треугольника, проведенная из вершины острого угла, проходит вне треугольника и пересекает продолжение стороны, к которой проведена.
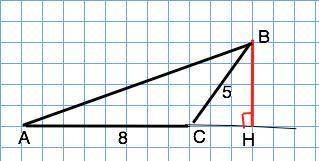
В ∆ АВС проведенная к стороне, равной 8 см, высота ВН=2•16:8=4. Тогда в "египетском" треугольнике ВСН отрезок СН=3 ( то же получим по т.Пифагора).
Треугольник АВН - прямоугольный, АН=8+3=11. По т.Пифагора его третья сторона АВ=√(АН²+BH²)=√(11²+4²)=√137
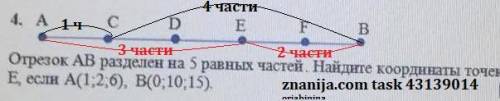
Отрезок АВ разделён на 5 равных частей. Найдите координаты точек С и Е, если А ( 1; 2; 6), В(0; 10; 15) .
Объяснение:
1) Для точки С имеем λ= 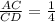 =0,25 .
=0,25 .
x(C)= 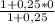 =1:1,25=0,8 ,
=1:1,25=0,8 ,
у(C)= 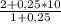 =4,5:1,25=3,6 ,
=4,5:1,25=3,6 ,
z(C)= 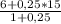 =9,75:1,25=76,8 . Значит С( 0,25 ; 3,6 ; 7,8)
=9,75:1,25=76,8 . Значит С( 0,25 ; 3,6 ; 7,8)
2) Для точки Е имеем λ= 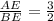 =1,5 .
=1,5 .
x(E)= 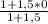 =1: 2,5=0,4 , у(E)=
=1: 2,5=0,4 , у(E)= 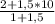 =17 : 2,5=6,8
=17 : 2,5=6,8
z(E)= 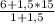 =9,75: 2,5=11,4 Значит С( 0,4 ; 6,8 ; 11,4) .
=9,75: 2,5=11,4 Значит С( 0,4 ; 6,8 ; 11,4) .
========================
х=(х₁+λх₂):(1+λ) ,у=( у₁+λу₂):(1+λ) ,где (х₁;у₁), (х₂;у ₂) -координаты концов отрезка , (х;у)-координаты точки, делящей отрезок в заданном отношении.
x<6+4
6<x+4
4<6+x