квадрат.
Объяснение:
Думаю, что задание звучало по-другому:
"Начертить четырёхугольник, у которого есть минимум 3 прямых угла, и две последовательные стороны имеют одинаковую длину"
Если это так, то рассуждаем следующим образом.
1. Сумма углов четырёхугольника равна 360°. Три из них по условию в сумме дали 270°, тогда и третий равен 90°, речь в задаче по определению идёт о прямоугольнике.
2. Смежные ( соседние, имеющие общую вершину) стороны этого прямоугольника, которые при изображении откладывают последовательно друг за другом, равные. Противолежащие стороны прямоугольника равны по свойству, тогда все стороны получатся равными, данный прямоугольник является квадратом.
ответ: необходимо начертить квадрат.
ответ: 45°
Объяснение:
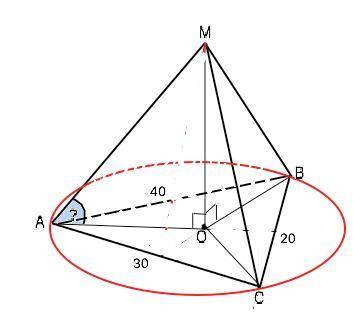
Если боковые ребра пирамиды равнонаклонены, т.е. угол наклона к основанию всех ребер одинаков, то её высота проходит через центр описанной около основания окружности.
Пусть в пирамиде МАВС МО - высота, АВ=40 см, ВС=20 см, АС=30 см. АО=ВО=СО=R.
Полупериметр ∆ АВС=45
Найденная по формуле Герона Ѕ(АВС)=√(45•5•15•25)=75√15.
Формула радиуса описанной около треугольника окружности R=a•b•c/4S, где a,b,c - стороны треугольника, S- его площадь.
R=(20•30•40):(4•75√15)=80/√15
Формула объема пирамиды V=h•S/3 ⇒ 2000=(h•75√15):3. Решив уравнение, получим h=80/√15
В прямоугольном треугольнике АSО катеты АО=SО=80√15. ⇒ tg(SAO)=1. Угол SAO=45°
отношения сторон не равны, треугольники не подобны.
Б) А=37°, В=48°, С=180-48-37=95°
Угол 1=48°, угол 2=95°
Треугольники подобны.
В) Уточните обозначения сторон второго тнеугольника.
Треугольник АВС
ВС=8 см - катет
АВ=10см - гипотенуза
АВ^(2)=АС^(2)+ВС^(2)
АС=6 см - катет
Треугольник 2
Если гипотенуза =5 см (уточните обозначения)
Катет 1 = 3 см
Катет 2 = 4 см ( теорема пифагора)
Отношения сторон:
5/10=4/8=3/6
Треугольники подобны