Задача 1.
Угол В 90 градусов, значит угол А плюс Угол С = 180-90=90 градусов.
Сумма (уменьшенных в два раза биссектрисами) углов при вершинах А и С в треугольнике АОВ будет в два раза меньше, т.е. 90:2= 45 градусов.
Сумма углов в треугольнике = 180 градусам, тогда искомый угол АОВ будет равен 180-45=135 градусов.
Задача 2.
В задаче дано, что угол при вершине В равен 60 градусов, при этом DBA = 30 градусам (получается половина 60ти), получается, что DB - биссектриса. Особенным свойством биссектрисы является то, что каждая точка биссектрисы равноудалена от сторон угла. Расстояние до стороны ВА дано и равно 4 (отрезок DA), расстояние от точки Д до стороны СВ будет таким же, т.е. 4.
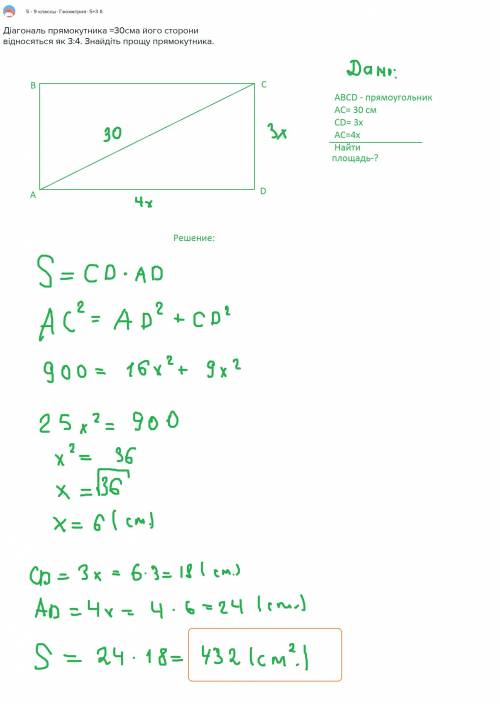
Задание 3(Первое фото)
Задание 4
67градусов и 30 минут=45 градусов + 22 градуса 30 минут.
1. Строите развернутый угол (180 градусов). С циркуля и линейки делите его пополам. Получаете угол в 90 градусов.
2. Аналогичным образом угол в 90 градусов делите пополам, получаете два смежных угла по 45.
3. Один из этих углов оставляете в покое, другой аналогично делите пополам. Это будут два угла по 22 градуса 30 минут.
4. Один из полученных маленьких углов и оставленный в покое угол в 45 градусов дадут в сумме 67 градусов 30 минут.
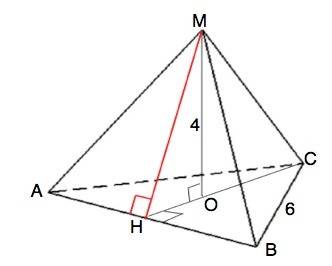
Пирамида правильная. Значит, основанием данной пирамиды является правильный многоугольник, а вершина проецируется в центр этого многоугольника.
Апофемой называется высота боковой грани, проведенная из вершины правильного многогранника.
Центр правильного треугольника - точка пересечения его высот, являющихся в правильном треугольнике медианами и биссектрисами.
а)
На рисунке в приложении О - центр основания. СН - высота ( медиана). Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины.
Следовательно, отрезок СО=2/3 высоты СН, отрезок ОН=1/3 высоты СН.
Все углы правильного треугольника равны :180°:3=60°
CН=СВ•sin60°=6•√3/2
CO=6√3/6=√3
ОН перпендикулярна АВ и является проекцией МН на плоскость АВС. По теореме о трёх перпендикулярах МН⊥АВ. =>
МН высота ∆ АМВ, т.е. апофема данной правильной пирамиды.
Высота пирамиды перпендикулярна основанию. => МО⊥СН.
Из прямоугольного ∆МОН по т.Пифагора
МН=√(МО²+НО²)=√(16+3)=√19 (ед. длины)
б)
Все боковые грани правильной пирамиды - равные равнобедренные треугольники. => их площади равны.
S (AMB)=MH•AB:2=√19•6:2=3•√19
S(бок)=3•3√19=9√19 (ед. площади)