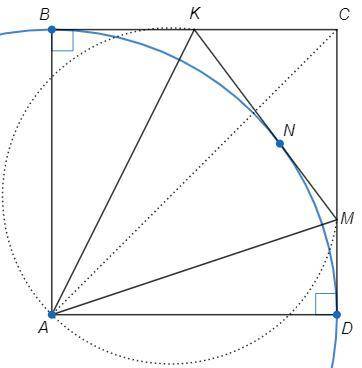
Найдем центр вневписанной окружности KCM.
Угол между биссектрисами внешних углов при K и M равен 90 -С/2 =45.
Отрезок KM виден из центра под углом 45.
Центр лежит на биссектрисе угла С.
Точка A является искомым центром т.к. удовлетворяет обоим условиям.
В, D - точки касания на продолжениях сторон (радиусы в эти точки перпендикулярны касательным).
Точка касания вневписанной окружности со стороной треугольника (N) делит периметр пополам.
(Отрезки касательных из одной точки равны: CB=CD, KB=KN, MN=MD => CK+KN=CM+MN)
CB =CK+KN =(3+4+5)/2 =6
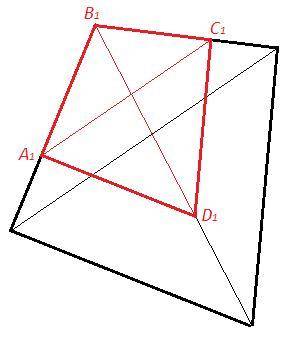
Соответствующие диагонали разбивают подобные многоугольники на подобные треугольники.
Доказываем подобие треугольников (с одинаковым коэффициентом и соответствием сторон) - тем самым доказываем подобие многоугольников.
(3) A1B1C1~ABC, A1D1C1~ADC (по двум сторонам и углу между ними)
(4) A1B1C1~ABC (по данным смежным сторонам и углу между ними)
A1D1C1~ADC (по стороне (A1C1, AC) и прилежащим углам)
(6) A1B1C1~ABC, A1B1D1~ABD (по трем пропорциональным сторонам)
∠C1A1D1=∠CAD
C1A1D1~CAD (по двум сторонам и углу между ними)
биссектриса ВМ делит его напополам ⇒△BMA равнобедренный, т.к. его углы А и М равны 30 градусам ⇒ АМ= 6 см
СМ - катет лежащий против угла 30 градусов и равен половине гипотенузы ВМ = 3 см ⇒
АС= АМ+МС=6+3=9 см