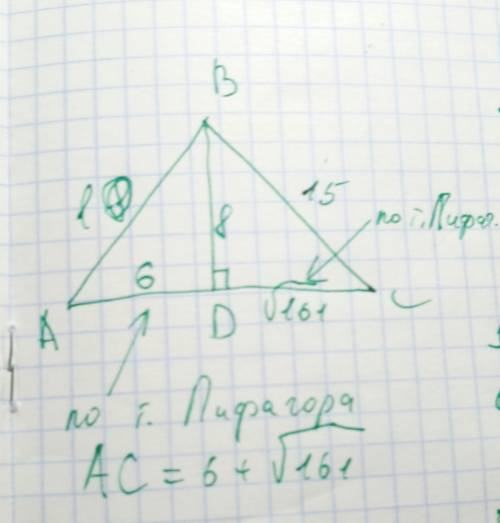
Объяснение:
1) Через любую точку пространства можно провести прямую, параллельную другой прямой, но при этом только одну. Данная тема называется параллельность прямых и плоскостей в пространстве.
2) Две плоскости называются параллельными, если они не пересекаются, то есть не имеют общих точек
3) 1°. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.2°. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны
4) Признак параллельности прямой и плоскости:
Если прямая, не лежащая в плоскости, параллельна какой-либо прямой, лежащей в плоскости, то эта прямая параллельна и самой плоскости.
1. Проведем произвольную прямую b, лежащую в плоскости α.
2. Через прямую b и точку М проведем плоскость β.
3. В плоскости β через точку М проведем прямую а, параллельную прямой b.
Прямая а будет параллельна плоскости α по признаку параллельности прямой и плоскости.
Задание №1.
ответ: Провести отрезок от точки М до точки К.
Объяснение: Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.
Задание №2.
ответ: МР = КТ.
Объяснение: Данные отрезки равны, так как прямые а и b - параллельные и отрезки МР и КТ образуют углы в 90°.
Задание №3.
ответ: АВ - гипотенуза треугольника АВН и сторона треугольника АВС; АН - катет треугольника АВН и высота треугольника АВС; АС - гипотенуза треугольника АСН и сторона треугольника АВС.
Задание №4.
ответ: 1) Нет, расстояние от точки А до прямой ВС построено не верно. 2) Расстояние от точки В до АН равно 2 см.
Объяснение: 1) Верно будет провести отрезок от точки А до С, тогда это будет верное расстояние.
Задание №5.
ответ: Расстояние от М до АВ равно 10.
Объяснение: В прямоугольном треугольнике, если угол равен 45°, значит два угла будут по 45°, один естественно 90°.
Получается это прямоугольный равнобедренный треугольник, отсюда следует, что два катета равны. А расстояние от точки М до АВ будет длина стороны МВ.
Задание №6.
ответ: Расстояние от М до ВА равно 6.
Объяснение: Проведём отрезок от от точки В до М, получится прямоугольный треугольник АВМ. Найдём длину гипотенузы АМ, она будет равна диаметру окружности, который равен двум радиусам. d = 2*R; d = 2 * 6; d = 12. Теперь по теореме катет лежащий против угла 30° равен половине гипотенузы, вычисляем ВМ = АМ / 2; ВМ = 12 / 2 = 6.
Задание №7.
ответ: Расстояние между ВС и AD равно 4 см.
Объяснение: Проведём высоту ВН на отрезок AD, так как это и будет расстоянием между ВС и AD. Получается прямоугольный треугольник АВН с ∠А = 30°. Отсюда следует ВН = AB / 2; BH = 8 / 2 = 4 см.
Задание №8.
ответ: Расстояние между красной и синей 3,6 см; между желтой и синей 7,2 см.
Объяснение: Расстояние между красной и синей равно 3 клетки, так как 1 клетка равна 1,2 см, нужно 3 * 1,2 = 3,6 см. Это и будет искомым расстояние. Точно также и с желтой и синей, расстояние между ними равно 6 клеток, отсюда следует 6 * 1,2 = 7,2 см.
P.s. Надеюсь, что я правильно понял 8 задание и 1 клетка равна 1,2 см, иначе прощения