α = 45°
Объяснение:
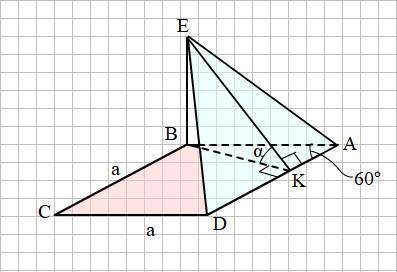
Смотри прикреплённый рисунок.
Из вершины В ромба проводим высоту ВК.
ВК = а · sin A = a · sin 60° = 0.5a√3.
Соединим точку Е с точкой К. ВК является проекцией наклонной ЕК на плоскость АВСD. Поскольку ВК - высота ромба. то ВК ⊥ AD.
По теореме о трёх перпендикулярах: если AD ⊥ BK (проекции наклонной ЕК), то AD⊥ ЕК. Следовательно, ∠ЕКВ = α является линейным углом, служащим мерой двугранного угла между плоскостями ADE и АВСD.
Найдём этот угол.
tg α = BE : BK = 0.5a√3 : 0.5a√3 = 1.
Следовательно, ∠α = 45°
1) Пусть в одной части х° , тогда величина первого угла равна х°, второго - (2х)°, третьего - (3х)°.
Зная, что сумма углов треугольника равна 180°, составим уравнение:
х + 2х + 3х = 180
6х = 180
х = 180 : 6
х = 30
∠1 = 30°, ∠2 = 60°, ∠3 = 90°.
2) В прямоугольном треугольнике напротив угла в 30° по теореме лежит катет, равный половине гипотенузы. В нашем треугольнике меньшей стороной, длина которой равна 4 см, как раз и является катет, лежащий напротив угла в 30°. Делаем вывод о том, что большая сторона, которой является гипотенуза , будет равна 4 см·2 = 8 см.
ответ: 8 см.