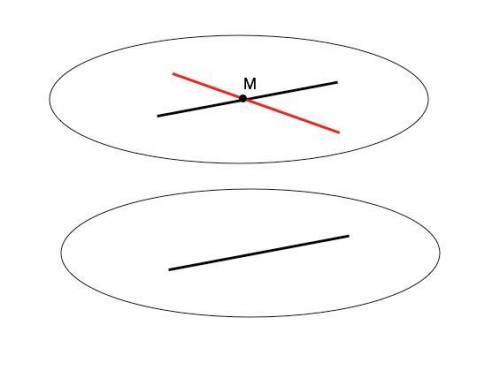
По условию данные две прямые не имеют общих точек с прямой а и пересекаются в т.М, значит, лежат в одной плоскости (свойство). Прямые в пространстве могут пересекаться, быть параллельными или скрещивающимися. Предположим, что ни одна из этих прямых не является скрещивающейся с прямой а. Так как они не пересекают прямую а ( не имеют с ней общих точек). обе параллельны прямой а. Но это допущение противоречит
Аксиоме параллельных прямых. Через любую точку, лежащую вне прямой, можно провести другую прямую, параллельную данной, и притом только одну.
⇒ Данные прямые не могут обе быть параллельными прямой а, поэтому хотя бы одна из них является скрещивающейся с прямой а
2). Дано:
a ⊥ c и b ⊥ c
_______________
a ║ b
Док-во
a ∩ c = A
b ∩ c = B
⇒ ∠A=∠B=90°
проведем перпендикуляр
d ⊥ a и d ⊥ b
a ∩ d = C
b ∩ d = D
⇒ ∠C=∠D=∠A=∠B=90°
⇒ ABCD - прямоугольник
⇒ a ║ b
ответ: ч.т.д.
3). Середина данного отрезка? какого отрезка?