Объяснение:
27. Все точки каждой из двух параллельных прямых равноудалены от
другой прямой.
Да, верно
28. Перпендикуляр, проведенный из точки к прямой, больше любой
наклонной, проведенной из этой же точки
к этой прямой.
Нет, не верно, поскольку перпендикуляр, проведённый к прямой из той же точки и к той же прямой, что и наклонная, всегда меньше наклонной
29. Внешний угол треугольника равен сумме двух внутренних углов, не
смежных с ним.
Да, верно. Теорема: внешний угол треугольника равен сумме двух внутренних углов треугольника не смежных с ним
Найдем второй отрезок гипотенузы для каждого случая.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.⇒
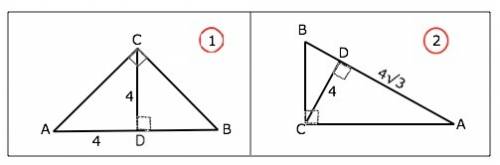
a)
СD²=АD•ВD
16=4•BD
BD=16:4=4⇒
Высота СD - медиана и биссектриса ∆ АВС и делит его на два равнобедренных прямоугольных треугольника.
Острые углы такого треугольника равны 45°
б)
СD²=АD•ВD
16=4√3•BD⇒
BD=16:4√3=4/√3
Из ∆ САD:
tg∠САD=CD:AD=4:4√3=1/√3- это тангенс 30°
Из ∆ CВD:
tg∠СBD=BD:CD=(4/√3):4=√3 - это тангенс 60°
Острые углы этого треугольника 30° и 60°
S = ( 0,5a + 0,5b ) * h
S = 0,5h( a + b )