x-угол А
угол В - х+35
угол с-х+10
х+10+х+35+х=180
х=45
угол В+80 и С + 50
cos∠B = 0
cos∠A = 0,6
cos∠C = 0,8
Объяснение:
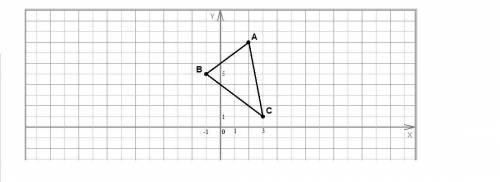
Найдем длины сторон треугольника по формуле расстояния между точками:
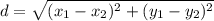
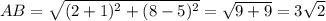
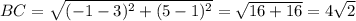

Проверим по теореме, обратной теореме Пифагора, не является ли этот треугольник прямоугольным:
AC² = AB² + BC²
(5√2)² = (3√2)² + (4√2)²
50 = 18 + 32
50 = 50 - равенство верно, значит треугольник прямоугольный с гипотенузой АС.
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
Косинус прямого угла равен нулю.
cos∠B = 0
cos∠A = AB / AC = 3√2 / 5√2 = 3/5 = 0,6
cos∠C = BC / AC = 4√2 / 5√2 = 4/5 = 0,8
пусть угол С=х,тогда угол В=25+х,а угол А=25+х-35
так как сумма углов треугольника=180, то
х+25+х+25+х-35=180
3х=165
х= 55(улол С)
угол В=80
угол А=45