Так как многоугольник - правильный, то все стороны и углы у этого многоугольника равны.
Сначала найдём количество сторон этого многоугольника.
Итак, угол правильного многоугольника вычисляется по формуле :
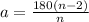
Где a - угол правильного многоугольника, n - количество сторон.
Подставим известные значения в формулу и узнаем численное значение переменной n :
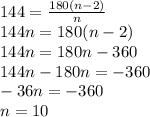
Количество сторон = 10.
2) Периметр многоугольника - сумма длин всех сторон.
Можно записать формулу для нахождения периметра правильного многоугольника так :
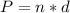
Где P - периметр, n - количество сторон, d - длина стороны.
Нам нужно найти d :
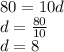
Сторона многоугольника = 8 см.
ответ: 8 см.
Объяснение:
№5
Вариант 1.
По теореме: отрезки касательных, проведенные из одной точки к окружности, равны.
Исходя из этого:
АК=СК
ВК=DK
Так как
АВ=АК–ВК
СD=CK–KD
То:
АВ=СD.
Вариант 2.
Вариант 2.Проведём АС и BD.
По теореме: отрезки касательных, проведенные из одной точки к окружности, равны.
Тогда:
СК=АК
КВ=КD
Углы АКС и ВКD равны как вертикальные. Пусть каждый из них равен Y.
Рассмотрим треугольник АКС
СК=АК
Тогда треугольник равнобедренный с основанием АС.
Тогда угол АСК=(180–Y)÷2
Рассмотрим треугольник ВКD.
КВ=КD
Тогда треугольник равнобедренный с основанием BD
Тогда угол BDK=(180°–Y)÷2
Следовательно угол BDK=угол АСK.
Тогда АС||ВD, а углы BDC и АСD накрест-лежащие при параллельных прямых АС и ВD и секущей СD.
Обозначим трапецию АВСD. Опустим высоты ВМ и СК из вершин углов при верхнем основании.
Четырехугольник МВСК - прямоугольник. МК=ВС=7.
Примем АМ=х. Тогда КD=AD-AM-7=12-х-7=5-х
По т.Пифагора
ВМ²=АВ²-АМ²=9-х²
CК²= СD²-KD²=16-25+10х-х² = -9+10х-х²
Так как ВМ =СК, то
9-х²= -9+10х-х², откуда
10х=18.
х=1,8 (ед. длины)
Из ∆ АВМ
ВМ=√(9-3,24)=2,4 (ед. длины)