Исследуемый четырехугольник - трапеция, подобная данной. Площади подобных фигур относятся друг к другу как квадраты их линейных размеров.
Высота данной трапеции равна sqrt[((24 - 12)/2)^2 + 10^2] = 8.
Площадь данной трапеции равна (12 + 24)*8/2 = 144.
Радиусы вписанных окружностей равны 1, в высоте их вмещается два. Следовательно, высота искомой трапеции равна 8 - 1 - 1 = 6. Высоты этих трапеций относятся как 6/8 = 3/4. Значит, площади трапеций будут относиться друг к другу как 9/16.
И площадь искомого четырехугольника будет равна 144*9/16 = 81.
ответ: 81.
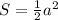
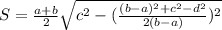
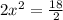
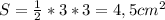
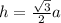
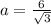
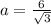
b+57=2((S/b)+b); b+57=(2S+b^2)/b; b^2+57b=2S+2b^2; b^2-57b+680=0;
D= 57^2-4*680=529;
X= (57+23)/2=40 - правильный корень. Подставляем P= 40+57=97;
97=2(a+40); 97=2a+80; 2a=17; a= 8,5; b= 40. Делаем проверку S=8,5*40=340