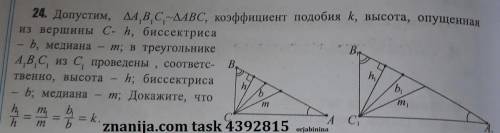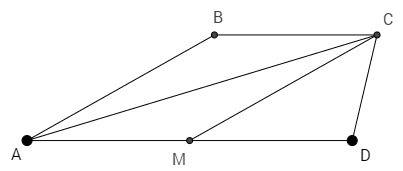
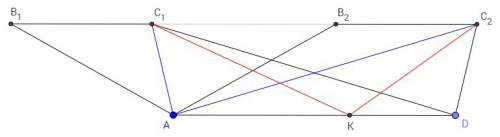
ABC ~ A1B1C1, высота из точки C - h, биссектриса - b, медиана - m. В треугольнике A1B1C1, соответственно, h1,b1,m1. Докажите, что h1/h = m1/m = b1/b = k.
Объяснение: Т.к. ABC ~ A₁B₁С₁ то
- сходственные стороны пропорциональны 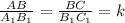 (@) ⇒
(@) ⇒ 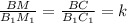 (**) , тк М-середина АВ;
(**) , тк М-середина АВ;
- соответственные углы равны ∠В=∠B₁ ⇒ половины этих углов тоже равны ∠ВСК=∠B₁С₁К₁ (*).
1) ΔСВН ~ ΔС₁В₁Н ₁ по 2-м углам : ∠В-общий , ∠СНВ =∠С₁Н₁В₁=90° ⇒ сходственные стороны пропорциональны 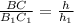 .
.
2) ΔСВК ~ ΔС₁В₁К ₁ по 2-м углам : ∠В-общий , ∠КСВ =∠К₁С₁В₁ ( см *) ⇒сходственные стороны пропорциональны 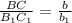 .
.
3) ΔСВM ~ ΔС₁В₁M ₁ по 2-м пропорциональным сторонам и равному углу между ними : ∠В-общий , 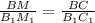 ( см **) ⇒сходственные стороны пропорциональны
( см **) ⇒сходственные стороны пропорциональны 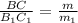 .
.
Итак, учитывая п. 1)2)3) получили
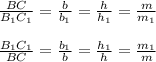 ,учитывая (@) получаем ,
,учитывая (@) получаем ,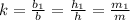 .
.