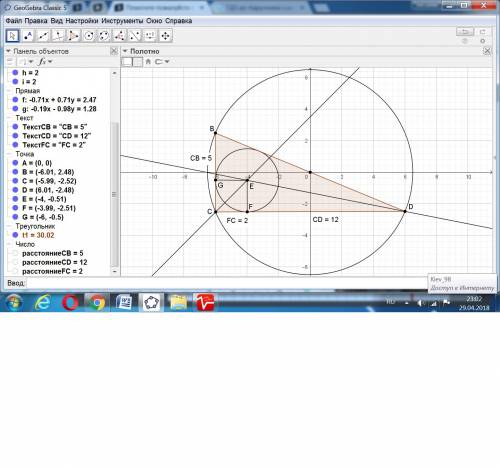
Пусть есть треугольник с катетами AB и BC.
Если радиус описанной окружности равен 6,5, то гипотенуза равна 2*6,5 = 13.
Отрезки катетов до точки касания вписанной окружности равны 2 и -2.
По свойству касательных гипотенуза равна сумме этих отрезков:
AB - 2 + BC - 2 = 13 или AB + BC=17.
За теоремой Пифагора 13² = AB² + BC².
Возведём в квадрат равенство AB + BC = 17:
AB² + 2AB*BC + BC² = 289. Заменим AB² +BC² = 169.
2AB*BC = 289 - 169 = 120, AB*BC = 120/2 = 60.
Из выражения AB+ BC = 17 выразим BC = 17 - AB и подставим в AB*BC = 60.
Получим: AB(17 -AB) = 60 или 17*AB -AB² = 60.
Получили квадратное уравнение AB² - 17AB + 60 = 0.
Квадратное уравнение, решаем относительно AB.
Ищем дискриминант:
D=(-17)^2-4*1*60=289-4*60=289-240=49;
AB1=(√49-(-17))/(2*1)=(7-(-17))/2=(7+17)/2=24/2=12;
AB2=(-√49-(-17))/(2*1)=(-7-(-17))/2=(-7+17)/2=10/2=5.
ответ: катеты равны 5 и 12.
Площадь полного круга занимает все его 360°.
Для ответа на заданный вопрос нужно найти, какую часть от целого круга составляет сектор с центральным углом, равный данным дугам. Такова же будет и часть площади, которую этот сектор занимает в круге.
Чтобы вычислить, какую часть целого числа составляет другое число, нужно представить ответ в виде правильной дроби. Записываем искомую величину над дробной чертой, как числитель а целое - под ней ( знаменатель). Желательно по возможности ( и для наглядности) сократить дробь (то есть разделить числитель и знаменатель на общий множитель.
а)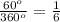
Какую часть от целого круга составляют оставшиеся три сектора и сектор с любой градусной мерой центрального угла, Вы без труда найдете самостоятельно.
Углы данной величины чаще всего встречаются в задачах по геометрии, и их доля от общего круга запоминается наизусть.