Построим отрезок BC длины a. Центр O описанной окружности треугольника ABC является точкой пересечения двух окружностей радиуса R с центрами в точках B и C. Выберем одну из этих точек пересечения и построим описанную окружность S треугольника ABC. Точка A является точкой пересечения окружности S к прямой, параллельной прямой BC и отстоящей от нее на расстояние ha (таких прямых две).
8.2.
Построим точки A1 и B1 на сторонах BC и AC соответственно так, что BA1 : A1C = 1 : 3 и AB1 : B1C = 1 : 2. Пусть точка X лежит внутри треугольника ABC. Ясно, что SABX : SBCX = 1 : 2 тогда и только тогда, когда точка X лежит на отрезке BB1, и SABX : SACX = 1 : 3 тогда и только тогда, когда точка X лежит на отрезке AA1. Поэтому искомая точка M является точкой пересечения отрезков AA1 и BB1.
8.3.
Пусть O — центр данной окружности, AB — хорда, проходящая через точку P, M — середина AB. Тогда |AP – BP| = 2PM. Так как РPMO = 90°, точка M лежит на окружности S с диаметром OP. Построим хорду PM окружности S так, что PM = a/2 (таких хорд две). Искомая хорда задается прямой PM.
8.4.
Пусть R — радиус данной окружности, O — ее центр. Центр искомой окружности лежит на окружности S радиуса |R ± r| с центром O. С другой стороны, ее центр лежит на прямой l, параллельной данной прямой и удаленной от нее на расстояние r (таких прямых две). Любая точка пересечения окружности S и прямой l может служить центром искомой окружности.
8.5.
Пусть R — радиус окружности S, O — ее центр. Если окружность S высекает на прямой, проходящей через точку A, хорду PQ и M — середина PQ, то OM2 = OQ2 – MQ2 = R2 – d2/4. Поэтому искомая прямая касается окружности радиуса
Ц
R2 – d2/4
с центром O.
8.6.
Возьмем на прямых AB и CD точки E и F так, чтобы прямые BF и CE имели заданные направления. Рассмотрим всевозможные параллелограммы PQRS с заданными направлениями сторон, вершины P и R которых лежат на лучах BA и CD, а вершина Q — на стороне BC (рис. 8.1). Докажем, что геометрическим местом вершин S является отрезок EF. В самом деле,
SR
EC
= PQ
EC
= BQ
BC
= FR
FC
, т. е. точка S
Фактически задача сводится к нахождению координат вектора CD.
Мы знаем, что СD перпендикулярно AB. И CD проходит через точку C.
Условие перпендикулярности -> косинус угла между векторами CD и AB равен нулю.
Формула косинуса угла между векторами - 
AB={-1+5;4-1}={4;3}
CD={x2-3;y2-2}
Составим уравнение прямой АВ: 
(*)
Подставляя вместо x1 и y1 в формулу косинуса 4 и 3 соответственно получим:
4(x2-3)+3(y2-2)=0
Также точка D принадлежит прямой AB, а значит x2 и y2 удовлетворяют уравнению (*).
Решаем полученную систему уравнений.
Мне лень решать - сами решите. Как найдёте x2 и y2 - подставьте их и найдите координаты вектора CD. Зная координаты направляющего вектора и точку, через которую проходит прямая, легко составить уравнение прямой.
Оно выглядит так: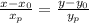 
, где 
- координаты напрвляющего вектора (в нашем случае вектора CD), а х0 и у0 - координаты точки, через которую проходит прямая (в нашем случае С или D - на выбор)
ΔABC : AB = BC; CD - биссектриса. ∠ADC = α
ΔABC - равнобедренный ⇒
∠BAC = ∠BCA ⇒ ∠ACD = 1/2 BCA = 1/2 BAC
ΔADC
∠ADC + ∠BAC + ∠ACD = 180°
α + ∠BAC + 1/2 ∠BAC = 180°
3/2 ∠BAC = 180° - α
∠BAC = (180° - α)*2/3
∠BAC = 120° - 2/3 α ∠BCA = ∠BAC = 120° - 2/3 α
∠B = 180° - (∠BCA + ∠BAC) = 180° - 2*(120° - 2/3 α) =
= 180° - 240° + 4/3 α = 4/3 α - 60°
ответ: ∠BCA = ∠BAC = 120° - 2/3 α; ∠B = 4/3 α - 60°
Для решения 1 и 2 пунктов достаточно в полученные формулы вместо α подставить соответствующие углы 60° и 75°
1. ΔABC : AB = BC; CD - биссектриса. ∠ADC = 60°
∠BCA = ∠BAC = 120° - 2/3 * 60° = 120° - 40° = 80°
∠B = 4/3 * 60° - 60° = 20°
ответ: ∠BCA = ∠BAC = 80°; ∠B = 20°
2. ΔABC : AB = BC; CD - биссектриса. ∠ADC = 75°
∠BCA = ∠BAC = 120° - 2/3 * 75° = 120° - 50° = 70°
∠B = 4/3 * 75° - 60° = 40°
ответ: ∠BCA = ∠BAC = 70°; ∠B = 40°