Объяснение:
1)АМ - гипотеза, ВМ-катет против угла 30*,тогда
ВМ=1/2 ВМ=26:2=13
2)<А=90-60=30*,тогда ВМ-катет против угла 30*,ВМ=30:2=15
5)∆АВС - равносторонний, все углы равны и высота является биссектрисой, <МАВ=30*
Расстояние от М до АВ - это перпендикуляр МК к стороне АВ и в ∆МКА МК является катетом против угла 30* и МК=МА:2=8:2=4
6) кратчайшее расстояние от М до АВ - это высота из вершины М.
∆АВМ прямоугольный, равнобедренный и высота МН является медианой. Тогда по свойству медианы прямоугольного треугольника МН=8:2=4
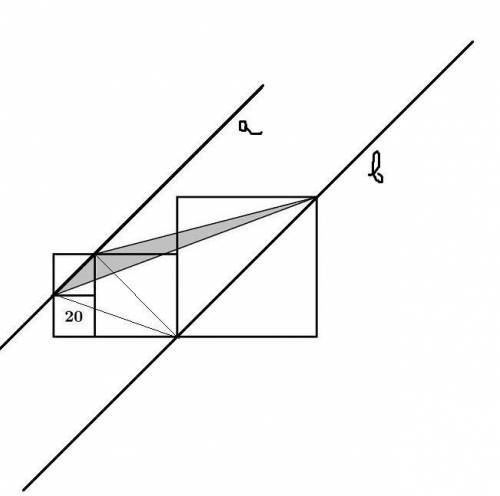
Рассмотрим множество треугольников, у которых две вершины расположены на диагонали маленького квадрата (на исходном рисунке в условии), а третья лежит на прямой, содержащей диагональ большого квадрата (см. мой рисунок). Заметим, что площади треугольников, входящих в это множество, попарно равны. Действительно, у всех треугольников общая сторона — диагональ малого квадрата, высоты, падающие на эту диагональ тоже равны, поскольку a ║ b.
Значит, площадь серого треугольника равна площади треугольника, указанного на моем рисунке. Площадь среднего квадрата равна 80. Теперь осталось следить за руками: (80+20+20)-40-10-60/2=70-30=40. Площадь равна 40.