ответ:
1.
пусть данный треугольник авс, ав> вс> са. угол асв=105, угол авс=15, угол вас=60. разделим св пополам (точка д) и востановим из этой точки перпендикуляр до пересечения с ав (точка к) , проведем отрезок ка. треугольник вкс - равнобедренный с углами у основания 15 град. построим дугу с центром в точке а и проходящую через точку с до пересечения с ав (точка м) треугольник амс равнобедренный и равносторонний с углом 60 град. но и треугольник смк тоже равнобедренный, т. к. угол мкс=углу ксм=30 град, а угол кмс=120 град. это легко устанавливается из своиств углов треугольников (сумма их равна 180 град) и своиства открытого угла.
объяснение:
1.
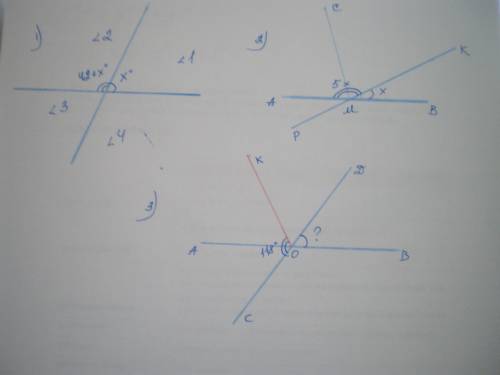
Пусть ∠1=х°, тогда ∠2=(42+х)°, что в сумме составляет 180° по определению смежных углов. Составим уравнение:
х+42+х=180; 2х=138; х=69.
∠1=∠3=69°; ∠2=∠4=69+42=111°.
2. Дано: ∠ВМК и ∠АМК - смежные, МС - биссектриса ∠АМК. Найти ∠СМК и ∠СМВ.
Пусть ∠ВМК=х°, тогда ∠АМК=5х°, что в сумме составляет 180°.
х+5х=180; 6х=180; х=30.
∠ВМК=30°, ∠АМК=30*5=150°
∠СМК=1/2 ∠АМК = 150:2=75°
∠СМВ=∠СМК+∠ВМК=75+30=105°
3. Дано: АВ и СD - прямые, ∠СОК=118°, ОК - биссектриса ∠АОD. Найти ∠ВОD.
∠КОD и ∠СОК - смежные, значит, их сумма составляет 180°.
∠КОD = 180-118=62°
∠АОК=∠КОD=62° (по определению биссектрисы)
∠АОК+∠КОD=62+62=124°
∠ВОD=180-124=56°
5х=90
х=18градусов
4х=72