Если катеты прямоугольного треуг в основании 3 и 4, то гипотенуза равно 5 см, т.к это египеnский треугольник.(ну или по т.Пифагора)
Большая грань будет основана на большей стороне треугольника. Т.е, квадрат со стороной 5см, а это значит, что высота призмы будет равно также 5.
Soсн= a*b/2=3*4/2=6см^2
V призмы=S основания * H=6cм^2 * 5см = 30 cм^3
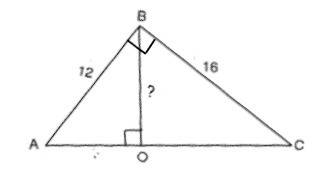
По т.Пифагора найдём гипотенузу.
АС=√(BC²+AC²)=√(256+144)=20 см
Высоту BO проще всего найти из площади треугольника.
S=BC•AB/2
S=BO•AC/2 Следовательно,
BC•AB=BO•AC, откуда
BO=BC•AB:AC
BO=16•12:20=9,6 см
-----
Вариант решения ( несколько длиннее) - его алгоритм дан ниже.
1) Находим гипотенузу по т.Пифагора
2) Катет прямоугольного треугольника – среднее пропорциональное между гипотенузой и проекцией этого катета на неё. ⇒
АВ²=АС•АО, ⇒ АО=АВ²:АС Отрезок СО находим вычитанием АО из гипотенузы или тем же что АО.
3) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу. ⇒
ВО²=СО•АО. Вычисления дадут ту же длину ВО=9,6 см
ответ:100 см²
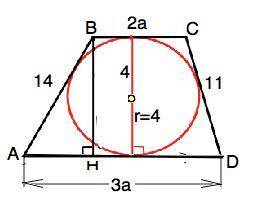
Объяснение: В четырехугольник можно вписать окружность ( или круг) тогда и только тогда. когда суммы противоположных сторон равны.
Трапеция АВСD - четырехугольник. ⇒
ВС+АD=АВ+AD=14+11=25 (см).
Высота трапеции равна диаметру вписанной окружности. ⇒ ВН=2r=2•4=8
Площадь трапеции равна произведению высоты и полусуммы оснований.
S=h•(a+b)/2=8•25/2=100 см².
----------------------
Как видим, для нахождения площади отношение оснований трапеции является лишним. Но для нахождения длин сторон пригодится.
Примем коэффициент отношения ВС:АD равным а.
Тогда ВС=2а, АD=3а.
ВС+АD=5a=25 (см. выше). ⇒ а=5. ⇒
ВС=2•5=10 см
АD=3•5=15 см.
Vпризмы=Sh
Площадь прямоуг.треугольника равна половине произведения катетов
S = 3 * 4 : 2 = 6(см2) - площадь основания
Корень из 4^2 + 3^2 = 5(cм) - гипотенуза треугольника,является стороной квадрата и высотой призмы
V=6 * 5 = 30(cм3)
ответ: объем призмы 30см3