Question

Прикрепите !

высота правильной четырехугольной призмы равна 18 см, а диагональ призмы образует с плоскостью ее основания угол 60 °. найдите сторону основания призмы и угол, который диагональ призмы образует с ее боковой гранью.

Answer 1

$AD=\frac{18}{\sqrt{6}}$

∠$A_{1}DB_{1} = arcsin(\frac{\sqrt{2} }{4})$

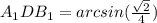
Объяснение:

Призма ABCDA₁B₁C₁D₁, ∠B₁DB=60°, BB₁=18см. AD=? ∠A₁DB₁=?

1) Правильная четырехугольная призма => ABCD - квадрат, BB₁D - прямоугольный треугольник (∠DBB₁=90°)

ABCD - квадрат => В ΔABD ∠DAB=90° =>BD²=AD²+AB²

AD=AB=A₁B₁=x, BD=y, B₁D=z =>

$x^{2} +x^{2} =y^{2} = 2x^{2} =y^{2} = y=x\sqrt{5} = x=\frac{y}{\sqrt{2} } \\cosB_{1} DB=\frac{BD}{B_{1} D} =\frac{y}{z} = \frac{y}{z} =cos(60^{o} )=\frac{1}{2} = y=\frac{z}{2} \\sinB_{1} DB=\frac{BB_{1}}{B_{1} D} =\frac{18}{z} = \frac{18}{z} =sin(60^{o} )=\frac{\sqrt{3} }{2} = z=\frac{18*2}{\sqrt{3} } \\=y=\frac{18*2}{2\sqrt{3} } =\frac{18}{\sqrt{3} }\\= x=\frac{18}{\sqrt{3}*\sqrt{2}}=\frac{18}{\sqrt{6}}$

2) Угол между диагональю и гранью  - угол между диагональю и её проекцией на эту грань. A₁D - проекция диагонали B₁D на AA₁D₁D => нужно найти ∠A₁DB₁

Правильная четырехугольная призма =>A₁B₁ ⊥AA₁D₁D => В ΔA₁B₁D ∠B₁A₁D=90° =>

$sinA_{1} DB_{1} =\frac{A_{1}B_{1}}{B_{1}D} =\frac{x}{z} =\frac{18}{\sqrt{6} * \frac{\sqrt{3} }{18*2} } =\frac{1}{2\sqrt{2} } =\frac{\sqrt{2} }{4} = A_{1} DB_{1} =arcsin(\frac{\sqrt{2} }{4})$