Грань АА1С1С - квадрат.
АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.
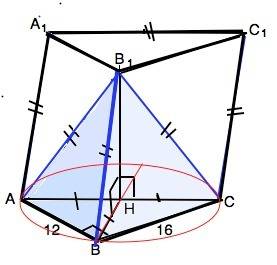
По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒
Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы.
∆ АВС прямоугольный, R=АС/2=10.
АН=СН=ВН=10.
Высота призмы совпадает с высотой В1Н пирамиды.
По т.Пифагора
В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3
Формула объёма призмы
V=S•h где S - площадь основания, h - высота призмы.
S-12•16:2=96 (ед. площади)
V=96•10√3=960√3 ед. объёма.
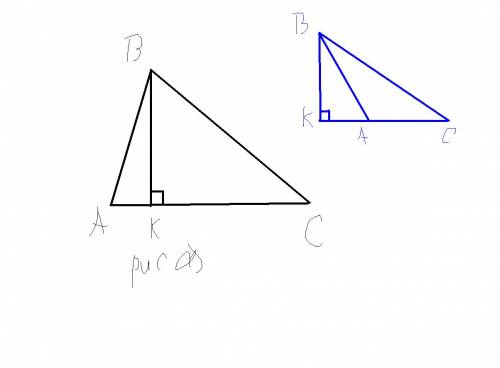
Нехай (рис.а) АВС - даний трикутник, ВК - його висота, опущена на сторону АС, ВК=2 м, АК=3м, СК=10 м,
Основа АС=АК+СК=3+10=13 м
Площа трикутника дорівнює половині добутку його основи на висоту, опущеної на неї.
[tex]S_{ABC}=\frac{1}{2}*AC*BK=0.5*13*2=13[/tex ] кв.м
відповідь: 13 кв.м
Нехай (рис.б) АВС - даний трикутник, ВК - його висота, опущена на сторону АС, ВК=2 м, АК=3м, СК=10 м,
Основа АС=СК-АК=10-3=7 м
Площа трикутника дорівнює половині добутку його основи на висоту, опущеної на неї.
[tex]S_{ABC}=\frac{1}{2}*AC*BK=0.5*7*2=7[/tex ] кв.м
відповідь: 7 кв.м
Для начала ставите точку А, проводите от неё луч. Отмечаете на луче точку С так, чтобы отрезок АС был равен 5 см. Прикладываете транспортир на луч крестиком (или дырочкой, транспортиры разные) в точку А. Смотрите, где будет угол в 60 градусов, делаете пометку - точка В. Соединяете точку А с точкой В. Отрезок АВ должен равняться 4 см, лишнее стираете. Соединяете точку В с точкой С. Угол А отмечаете дугой.
Вершины названы (A, В, С), угол отмечен, треугольник готов.