Відповідь: 2π см або 6,28 см
Пояснення:
Дано :ΔАВС, АВ=6 см, ∠А=100°, ∠В=50°
Знайти: ∪АВ-?
Рішення:
Проти меншого кута лежить менша сторона, отже менший кут спираєтьсяна найменшу дугу.
За теоремою про суму кутів трикутника
∠А+∠В+∠С=180°
100°+50°+∠С=180°
∠С=180°-150°
∠С=30°
Отже ∪АВ- найменша, а ∠С- вписаний кут.
∠ АОВ- центральний- він = 60° (Вписаний кут дорівнює половині центрального кута)∠С=1/2 ∠АОВ → ∠АОВ=2∠С=2*30°=60°
Розглянемо ΔАОВ, де АО=ОВ= r , ∠АОВ=60°, так як кути при основі рівнобедреного трикутника рівні, то ∠ВАО=∠АВО
2∠ВАО+∠АОВ=180°( за теоремою про суму кутів Δ)
∠ВАО=∠АВО =(180-°60°):2=60°.
Всі кути рівні, отже ΔАОВ- рівносторонній АО=ОВ=АВ=r=6 cм
довжина дуги:
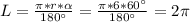 (cм)≈2*3,14≈6,28 см
(cм)≈2*3,14≈6,28 см
ответ:
Задача некорректно составлена.
Решение 1)
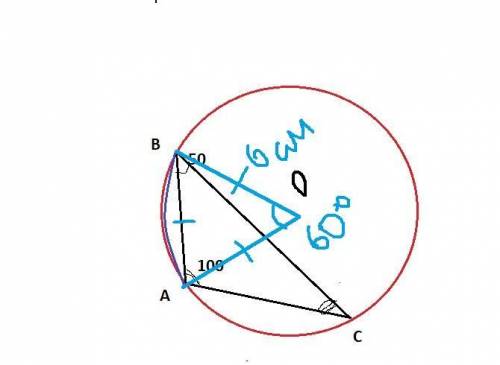
Используем угол при основании трапеции ∠W.
Сумма углов прилежащих к боковой стороне трапеции равна 180°
∠W+∠X=180°, свойство трапеции.
∠W=180°-∠X=180°-150°=30°
Проведем высоту ХН.
∆ХНW- прямоугольный треугольник
ХН- катет против угла ∠W=30°
XH=XW/2=9/2=4,5ед.
S(XYZW)=XH(XY+WZ)/2=4,5(11+13)/2=4,5*24/2=54ед²
ответ: 54ед²
Решение 2)
Используем т.Пифагора ∆XWY.
XY=HZ=11
WH=WZ-HZ=13-11=2
Теорема Пифагора
ХН=√(ХW²-WH²)=√(9²-2²)=√(81-4)=
=√77
S(XYZW)=XH*(XY+WZ)/2=
=√77(11+13)/2=√77*24/2=12√77
ответ: 12√77 ед²
25 х² = 16х² + 81
9х² = 81
х² = 9
х = 3
Значит второй катет равен 4 * 3 = 12
а гипотенуза 5 * 3 = 15
Радиус описанной окружности равен половине гипотенузы
R = 15 : 2 = 7,5см
2) Предположим, что проекция катета равного 4 см на гипотенузу равна х см, тогда по соотношениям в прямоугольном треугольнике
4² = х * (х +6), получим квадратное уравнение
х² + 6х - 16 = 0. по теореме обратной к теореме Виета. Получим корни
х₁ = 2 и х₂ = -8(второй корень не подходит по условию задачи).
Значит гипотенуза равна 2 +6 = 8 см, а высота h² = 2 * 6 = 12
h = √12 = 2√3cм