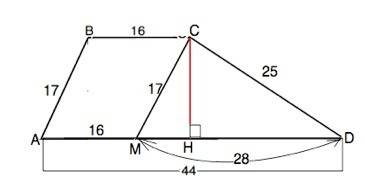
Назовем трапецию АВСD. АВ=17 см, ВС=16 см, СD=25 см, AD=44 см
Площадь трапеции равна произведению её высоты на полусумму оснований. Основания даны, высоту надо найти.
Один из решения:
Проведем СМ параллельно ВА. СМ=17 см (или ВК параллельно СD. Тогда ВК=25).
Получим треугольник, в котором известны три стороны: 17, 25 и 28 см.
По ф. Герона площадь этого треугольника равна 210 см².
Высота СН является и высотой трапеции.
S(∆ MCD)=CH•MD:2⇒
CH=2•S:MD=420:28=15 см
S(ABCD)=CH•(BC+AD):2=15•30=450 см²
1 - д. 2 - д 3 - д.
Объяснение:
1. Точка может быть центром бесконечного числа концентьрических окружностей (окружностей разных радиусов).
2. Через одну точку можно провести бесконечное число пересекающихся (или касающихся) окружностей.
3. Так как через три точки можно провести единственную окружность, а даны только 2 точки, то третья точка может располагаться в любом месте. Значит через две точки можно провести бесконечное число пересекающихся (имеющих две общие точки) окружностей. Центры этих окружностей будут лежать на серединном перпендикуляре к отрезку АВ.