Длина картона кратна и ширине, и длине карточки:
48:16=3, 48:12=4. Ширина картона НЕ кратна ни длине, ни ширине карточки.
По ширине нужно разметить первую линию разреза так, чтобы оставшаяся часть картона по ширине была кратна одному из размеров карточки.
Если отрезать первую полосу шириной 16 см, ширина оставшейся части картона будет 28 - не кратна ни одному размеру карточки.
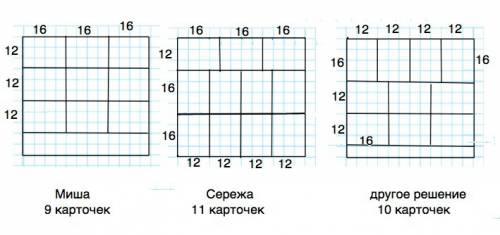
Следовательно, сначала нужно отрезать от картона полоску шириной в 12 см и разрезать на 3 части.
Оставшийся лист будет размером 32•48, и оба его размера теперь кратны длине карточки. Разрезав его по ширине на две полоски по 16 см, можно затем каждую разрезать на 4 карточки шириной 12 см, при этом излишков не образуется.
Если первую полоску отрезать шириной 16 см, ширина оставшейся части картона не будет кратной ни длине, ни ширине. Поэтому ее нельзя будет разрезать, чтобы не осталось лишнего картона.
Данный лист картона можно разрезать на 11 карточек, при этом не образуется излишков.
Геометрия - важный раздел математики. Ее возникновение уходит в глубь тысячелетий и связано прежде всего с развитием ремесел, культуры, искусств, с трудовой деятельностью человека и наблюдением окружающего мира. Об этом свидетельствуют названия геометрических фигур.
Например, название фигуры "трапеция" происходит от греческого слова "трапезион" (столик) , от которого произошли также слово "трапеза" и другие родственные слова. От греческого слова "конос" (сосновая шишка) произошло название "конус", а термин "линия" возник от латинского "линум" (льняная нить) .
Геометрические знания широко применяются в жизни - в быту, на производстве, в науке. При покупке обоев надо знать площадь стен комнаты; при определении расстояния до предмета, наблюдаемого с двух точек зрения, нужно пользоваться известными вам теоремами; при изготовлении технических чертежей - выполнять геометрические построения. И если ты, юный читатель, хорошо изучил курс геометрии, то не останешься безоружным, когда при решении практических задач потребуется применить геометрические теоремы или формулы.
tg B=AC/BC=5/(5√3)=1/√3
B=30 градусов.
Гипотенуза AB
AB=√(AC^2+BC^2)=√(5^2+5^2*3)=√100=10.
Если нужно без тригонометрии, то сначала находим гипотенузу, а потом угол В.
Катет АС против угла В равен половине гипотенузы, значит, угол В=30 градусов.