Объяснение:
A(1: - 2) , B( 3:6) , C(5;- 2)
1) Для того чтобы найти координаты вектора надо от координат конца вектора вычесть соответствующую координату начала вектора .
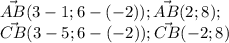
2) Координаты точки М -середины отрезка АВ находятся
по формулам :
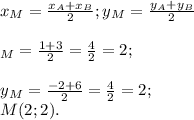
3) Найдем координаты вектора CM
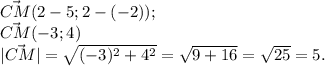
4) Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник является параллелограммом.
Пусть точка О ( x; y) - середина диагонали АС . Найдем ее координаты по формулам координат середины отрезка.
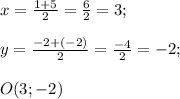
Найдем координаты середины диагонали BD
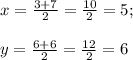
(5; 6) - середина диагонали BD
Так как координаты середин диагоналей не совпадают, то четырехугольник ABCD не является параллелограммом.
а) Доказательство:
АВ = ВМ, по условию, значит треугольник АВМ - равнобедренный. По свойству равнобедренного треугольника угол ВАМ = углу ВМА.
По свойству параллелограмма ВС параллельно АD, АС - секущая, значит угол АМВ = углу МАD, из вышесказанного следует, что угол ВАМ = углу МАD, значит АМ - биссектрисса
б) Решение:
АВ = СD по свойству параллелограмма,а АВ = ВМ из доказательства. Значит АВ = ВМ = СD = 8 см
МС = 4 по условию. ВС = ВМ + МС = 8 + 4 = 12. По свойству параллелограмма ВС = АD = 12
теперь можем найти площадь: Р = АВ + ВС + СD + DА = 8 + 12 + 8 + 12 = 40 см