108. АС = 3,6 см; СD = 6 cм; DB = 13.2 см; АВ = 22,8 см;
109. Меньший угол 36°, больший угол 144°
Объяснение:
108.
АС : CD : DB = 3 : 5 : 11
Пусть АС = 3х, тогда CD = 5x и DB = 11x
По условию
DB = CD + 7.2 см
или
11х = 5х + 7,2
6х = 7,2
х = 1,2 (см)
АС = 3 · 1,2 = 3,6 (см)
СD = 5 · 1.2 = 6 (cм)
DB = 11 · 1.2 = 13.2 (см)
АВ = AC + CD + DB = 3.6 + 6 + 13.2 = 22.8 (cм)
109.
Луч делит развёрнутый угол на два угла, отношение которых 1 : 4
Величина развёрнутого угла равна 180°.
Пусть меньший угол равен х, тогда больший угол 4х
Вместе они равны 5х
5х = 180°
х = 36°
4х = 4 · 36° = 144°
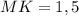 см
см
Объяснение:
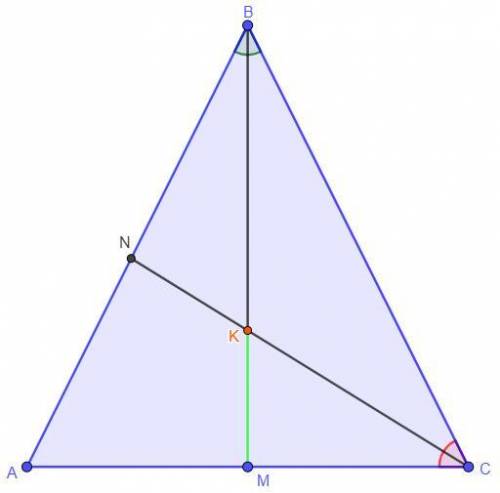
Дано: BM - медиана, биссектриса; CN - биссектриса, AB = BC = 5 см,
AC = 6 см
Найти: KM - ?
Решение: Так как по условию BM - медиана, то AM = MC = AC : 2 = 6 : 2 = 3 см. Так как по условию AB = BC, то треугольник ΔABC - равнобедренный. Так как треугольник ΔABC - равнобедренный, то медиана проведенная к основанию является высотой и биссектрисой по теореме. Треугольник ΔCMB является прямоугольным так как
BM ⊥ AC. BM = BK + KM ⇒ BK = BM - MK = 4 - MK.
Так как по условию CN - биссектриса, то по теореме о биссектрисе для треугольника ΔCMB:
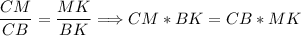
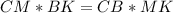
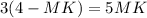
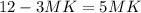
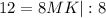
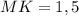 см.
см.
MT₁² + T₁P² = 5²
MT₁² + (T₁P+6)² = 9²
---
12*T₁P + 36 = 81 - 25
12*T₁P = 81 - 25 - 36 = 81 - 61 = 20
T₁P = 5/3 см
MT₁² + (5/3)² = 5²
MT₁² + 25/9 = 25
MT₁² + 25/9 = 25
MT₁² = (25*9 - 25)/9 = 200/9
MT₁ = 10√2/3 см
--- 2 ---
TM₁² + M₁P² = 6²
TM₁² + (M₁P+5)² = 9²
---
10*M₁P + 25 = 81 - 36
10*M₁P = 81 - 25 - 36 = 81 - 61 = 20
M₁P = 2 см
TM₁² + 2² = 6²
TM₁² + 4 = 36
TM₁² = 32
TM₁ = 4√2 см
--- 3 ---
ΔMPT₁ ~ ΔММ₁Н - один угол общий, второй прямой
НМ₁/РТ₁ = ММ₁/МТ₁
НМ₁/(5/3) = 7/(10√2/3)
НМ₁/5 = 7/(10√2)
НМ₁ = 5*7/(10√2) = 7/(2√2) см
--- 4 ---
ΔM₁PT ~ ΔТТ₁Н - один угол общий, второй прямой
НТ₁/РМ₁ = ТТ₁/ТМ₁
НТ₁/2 = (6+5/3)/(4√2)
НТ₁ = (18/3 + 5/3)/(2√2)
НТ₁ = 23/3/(2√2) = 23/(6√2) см
--- 5 ---
ΔРНМ₁
по теореме Пифагора найдём РН
РН² = НМ₁² + РМ₁²
РН² = (7/(2√2))² + 2²
РН² = 49/(4*2) + 4
РН² = 49/8 + 32/8
РН² = 81/8
РН = 9/(2√2) см
--- 6 ---
Площадь ΔТТ₁М через катеты и через гипотенузу и высоту к ней
S = 1/2*МТ₁*ТТ₁ = 1/2*МТ*Т₁Т₂
1/2*МТ₁*ТТ₁ = 1/2*МТ*Т₁Т₂
МТ₁*ТТ₁ = МТ*Т₁Т₂
МТ₁*ТТ₁ = МТ*Т₁Т₂
10√2/3*(6+5/3) = 9*Т₁Т₂
10√2/3*23/3 = 9*Т₁Т₂
Т₁Т₂ = 230√2/81 см--- 7 ---ΔТТ₁Т₂, по теореме Пифагора
Т₁Т₂² + ТТ₂² = Т₁Т²
(230√2/81)² + ТТ₂² = (23/3)²
ТТ₂² = 279841/81²
ТТ₂ = 529/81 см
--- 8 ---
Площадь ΔТМ₁М через катеты и через гипотенузу и высоту к ней
S = 1/2*ММ₁*ТМ₁ = 1/2*МТ*М₁М₂
1/2*ММ₁*ТМ₁ = 1/2*МТ*М₁М₂
ММ₁*ТМ₁ = МТ*М₁М₂
4√2*(5+2) = 9*М₁М₂
28√2 = 9*М₁М₂
М₁М₂ = 28√2/9 см--- 9 ---
ΔТМ₁М₂, по теореме Пифагора
М₁М₂² + ТМ₂² = М₁Т²
(28√2/9)² + ТМ₂² = (4√2)²
ТМ₂² = 16*2 - 784*2/81 = 1024/81
ТМ₂ = 32/9 см
--- 10 ---
Т₁К = Т₂М₂ = ТТ₂ - ТМ₂ = 529/81 - 32/9 = 241/81
Т₁К = 241/81 см
--- 11 ---
М₁К = М₂М₁ - Т₂Т₁ = 28√2/9 - 230√2/81 = √2/81*(28*9 - 230) = √2/81*(252 - 230) = 22√2/81 см
М₁К = 22√2/81 см
--- 12 ---
из ΔКТ₁М₁ по теореме Пифагора
Т₁М₁² = Т₁К² + М₁К²
Т₁М₁² = (241/81)² + (22√2/81)²
Т₁М₁² = (241² + 22²*2)/81²
Т₁М₁² = (58081 + 484*2)/81²
Т₁М₁² = 59049/81²
Т₁М₁² = 9
Т₁М₁ = 3 см