Объяснение:
ответ, проверенный экспертом
4,6/5
237
Владимир1111111
хорошист
12 ответов
3.4 тыс. пользователей, получивших
Пусть х- один угол, тогда второй - х+30. При пересечении диагоналей образуется прямоугольный треугольник с углом 90 градусом.
х+х+30+90=180
2х+120=180
2х=60
х=30
1 угол = 30 градусов, тогда 2 угол 2х30=60
Поскольку ромб это параллелограмм то он имеет все свойства параллелограмма, соответственно противолежащие углы равны. Тоесть, если 1 угол равен 30, то противолежащий угол тоже равен 30 градусов. С 2 углом тоже самое. ответ: 30, 60, 30, 60.
Такс, в ромбе диагональ выполняет функцию биссектрисы, значит 2х30=60, 2х60=120, потому что биссектриса делит углы пополам.
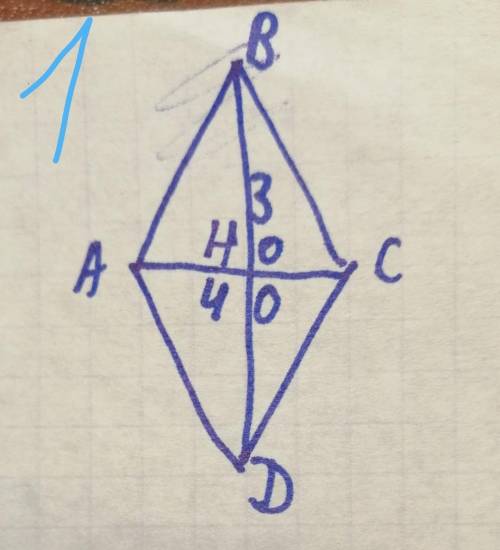
1). АС перпендикулярен ВD т.к. АВСD - ромб (Н - точка пересечения диагоналей)
ВН = НD = 30÷2 = 15
АН = НС = 40÷2 = 20
треуг. АНВ - прямоуг.
По т. Пифагора
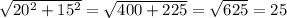
P = 25 * 4 = 100
ответ: 100
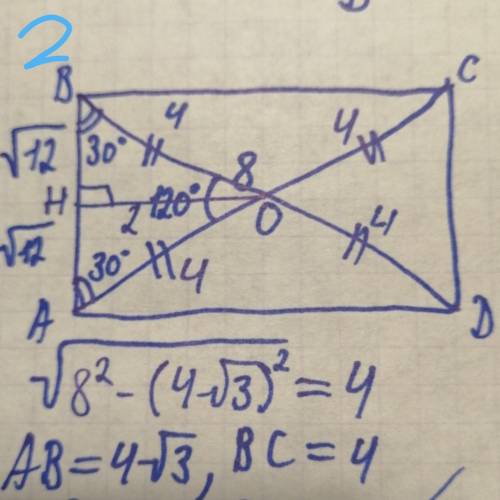
2). Проведем ОН перпендикулярно АВ
АО = ОС = ОВ = ОD (диагонали прямоугольника точкой пересечения делятся пополам)
угол ВОН = углу НОА = 60°
треуг. ВНО - прямоуг., угол НВО = 30° => ОН = 1/2 ОВ = 2
По т. Пифагора
НВ=
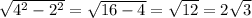
АВ = 2НВ = 4 корня из 3
треуг. АВD - прямоуг
По т. Пифагора
АD =
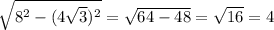
ответ: 2 стороны по 4 корня из 3, 2 стороны по 4
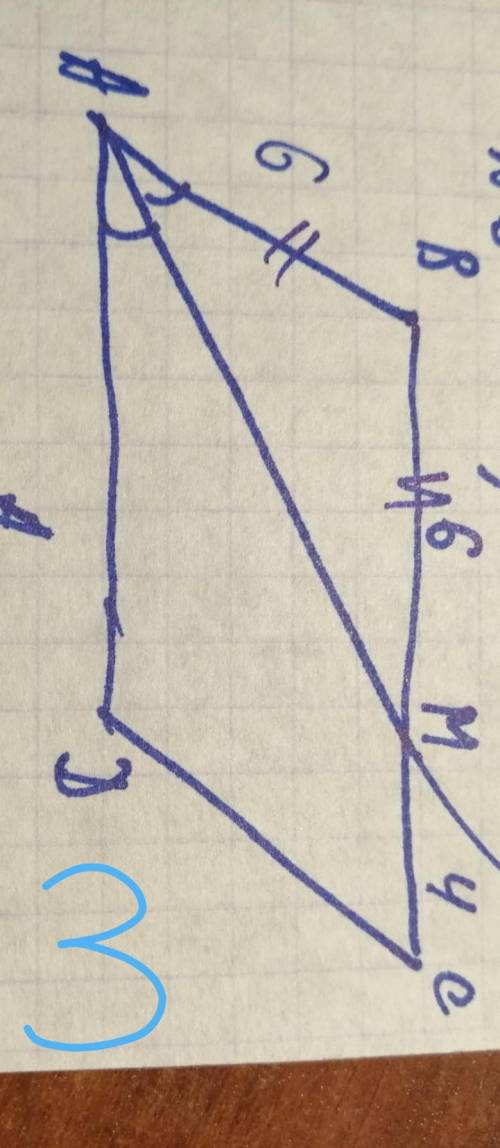
3). Биссектриса параллелограмма отсекает от него р/б треуг. => ВМ = АВ = 6
ВС = ВМ + МС = 6 + 4 = 10
Р = 6 + 6 + 10 + 10 = 32
ответ: 32
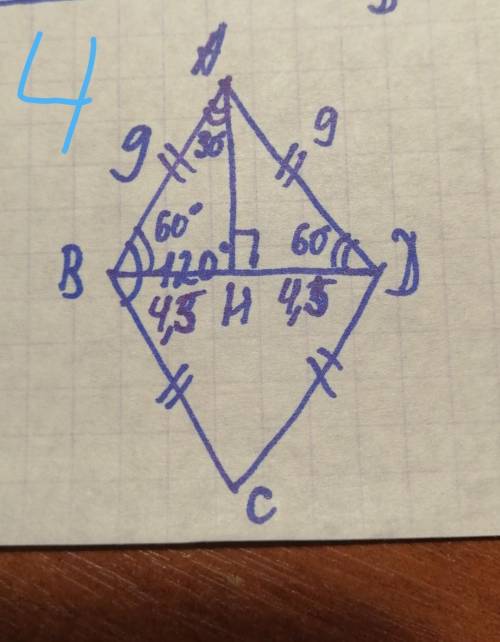
4). АВ = АD = 36÷4 = 9
Проведем АН перпендикулярно ВD
треуг. АВD - р/б, угол АВD = 120°÷2 = 60°
треуг. АВН - прямоуг., угол ВАН = 90° - 60° = 30° => ВН = 1/2 АВ = 4,5 (катет, лежащий против угла в 30°, равны половине гипотенузы)
ВD = 2ВН = 9
ответ: 9
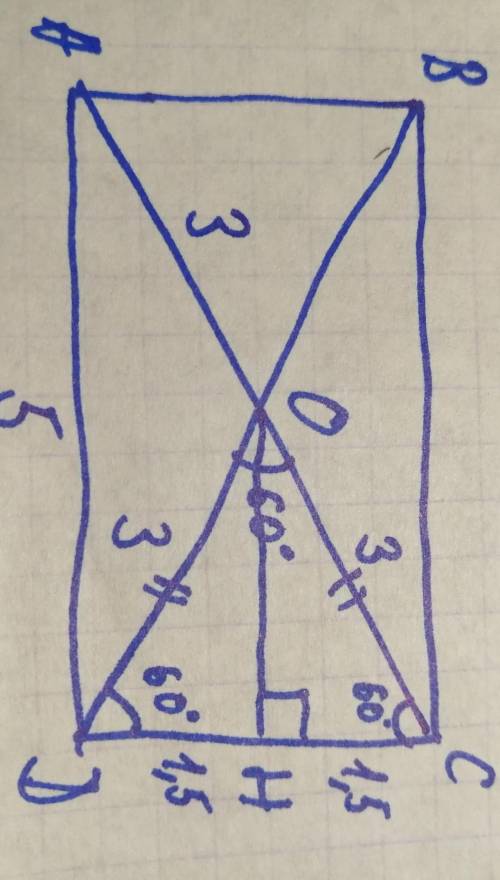
5). Проведем ОН перпендикулярно СD
угол СОН = углу HOD = 60°÷2 = 30°
треуг. СОН - прямоуг., угол СОН = 30° => СН = 1/2 ОС = 1,5 (катет, лежащий против угла в 30°, равны половине гипотенузы) => CD = 3
треуг. АСD - прямоуг.
По т. Пифагора
АD=
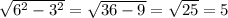
S = 3 * 5 = 15
ответ: 15
отсюда ВН =sin<A * AB
BH = 4/5 * 15 см =12 см
По формуле площади параллелограмма найдем АD=BC (тк противолежащие стороны паралл. равны) :
Sabcd= BC * BH
240= BC * 12
BC=АС= 20см
ответ: 20 см