Дано :
ΔАВС.
D ∈ AB.
E ∈ BC.
DE ║ AC.
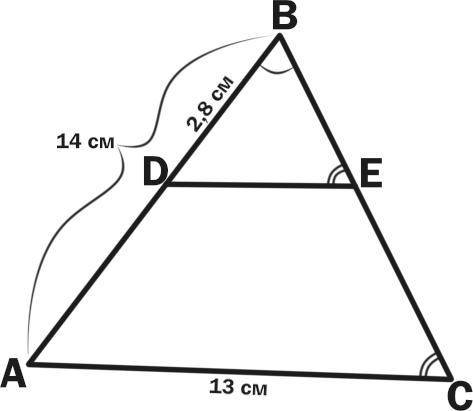
DB = 2,8 см.
АВ = 14 см.
АС = 13 см.
Найти :
ED = ?
Краткое -
∢BDE = ∢BАC, т. к. соответственные углы.
∢BЕD = ∢BCA, т. к. соответственные углы ⇒ ΔABС ∼ ΔDBЕ.
DE = 2,6 см.
Полное -
∠В - общий для ΔАВС и ΔDBЕ.
Рассмотрим соответственные ∠BED и ∠ВСА при пересечении параллельных прямых ED и АС секущей ЕС.
При пересечении двух параллельных прямых секущей соответственные углы равны.Тогда -
∠BED = ∠ВСА.
Следовательно, ΔАВС ~ ΔDBЕ по двум равным углам (первый признак подобия треугольников).
В подобных треугольниках против равных углов лежат сходственные стороны.Тогда пара сторон -
АВ и BD - сходственные стороны
АС и DE - сходственные стороны.
Отношения сходственных сторон подобных треугольников равны.То есть -
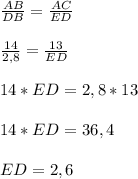
ED = 2,6 см.
2,6 см.
Объяснение:
Свойство биссектрисы угла треугольника. Решение треугольников. Вычисление биссектрис, медиан, высот, радиусов вписанной и описанной окружностей. Формулы площади треугольника: формула Герона, выражение площади треугольника через радиус вписанной и описанной окружностей.
Вычисление углов с вершиной внутри и вне круга, угла между хордой и касательной.
Теорема о произведении отрезков хорд. Теорема о касательной и секущей. Теорема о сумме квадратов сторон и диагоналей параллелограмма
Вписанные и описанные многоугольники. Свойства и признаки вписанных и описанных четырехугольников.
Геометрические места точек.
Решение задач с геометрических преобразований и геометрических мест.
Теорема Чевы и теорема Менелая.
Эллипс, гипербола, парабола как геометрические места точек.
Неразрешимость классических задач на построение.
Треугольникомназывается фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинамитреугольника, а отрезки - его сторонами.
Биссектриса
Биссектриса угла – это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Свойства биссектрис треугольника
· Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.
· Биссектрисы внутренних углов треугольника пересекаются в одной точке. Это точка называется центром вписанной окружности.
· Биссектрисы внутреннего и внешнего углов перпендикулярны.
· Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трех вневписанных окружностей этого треугольника.
· Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника.
Длина вектора:
ответ: 7