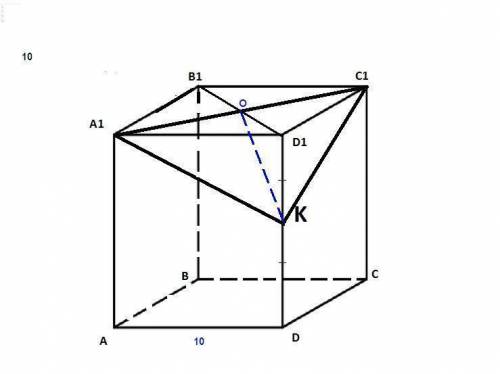
Соединяем точки А₁, С₁ и К, так как они попарно лежат в одной грани.
А₁С₁ = 10√2 как диагональ квадрата.
ΔА₁D₁K: по теореме Пифагора
А₁К = √(A₁D₁² + D₁K²) = √(10² + 5²) = √125 = 5√5
ΔA₁D₁K = ΔC₁D₁K по двум катетам (A₁D₁ = C₁D₁ как ребра куба, D₁K - общий), значит А₁К = С₁К = 5√5
Рa₁c₁k = 10√2 + 5√5 + 5√5 = 10√2 + 10√5 = 10(√2 + √5).
КО - медиана и высота равнобедренного треугольника А₁С₁К.
По теореме Пифагора:
КО = √(А₁К² - А₁О²) = √(125 - (5√2)²) = √(125 - 50) = √75 = 5√3
Sa₁c₁k = 1/2 · A₁C₁ ·KO = 1/2 · 10√2 · 5√3 = 25√6
Объяснение:<!--c-->
image
1. Так как дан правильный тетраедр, то независимо от данных граней искомое сечение будет являться равносторонним треугольником MNK. При построении этого сечения необходимо провести параллельные отрезки каждой стороне грани ADB, которая по определению правильного тетраэдра — равносторонний треугольник. Таким образом искомое сечение тоже является равносторонним треугольником, подобным треугольнику ADB.
2. Рассмотрим рисунок грани DCB, через центр O которой мы проводим сторону сечения NK.
image
3. Центр равностороннего треугольника находится в точке пересечения высот, биссектрис и медиан и делит медиану (которая также является высотой и биссектрисой) в отношении 2:1, другими словами отношение большой части медианы к всей медиане 2:3.
4. Значит, отношение стороны сечения к ребру тетраэдра также 2:3.
5. Если обозначить ребро тетраэдра через a и сторону сечения через b, то ba=23 и b=2a3.
6. Площадь равностороннего треугольника определяется по формулеSMNK=b2⋅3√4=4⋅a2⋅3√9⋅4=a2⋅3√9=32⋅3√9
7. В результате рассчётов, площадь сечения — SMNK=1⋅3√ см2.