Ребро не было указано в условии задачи, поэтому я обозначу его за {a}.
--------------
а)
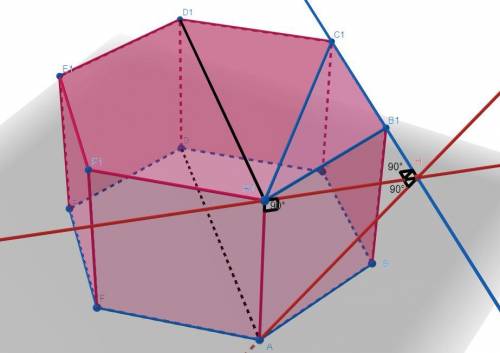
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
---------------
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.

A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)
-----------
теперь по теореме пифагора найдем AH:
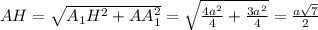
ответ: 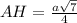
Во-первых, необходимо понять, какое из боковых ребер будет наибольшим. Для этого рассматриваются прямоугольные треугольники SAB, SAD, SAC. Так как у них есть общий катет SA, то наибольшая гипотенуза будет у треугольника с наибольшим вторым катетом (это очевидно следует из теоремы Пифагора). Так как диагональ квадрата всегда больше его стороны, то AC>AB=AD. Очевидно, что SC = 13 см - наибольшее боковое ребро.
SA вычисляется по теореме Пифагора для треугольника SAC.
Площадь квадрата находим по формуле: S = d^2 / 2 (d - длина диагонали).
Объем пирамиды равен 1/3 * S*H, где S - площадь основания, H - длина высоты. В нашем случае высота равна SA.
ответ: 50 см^3.