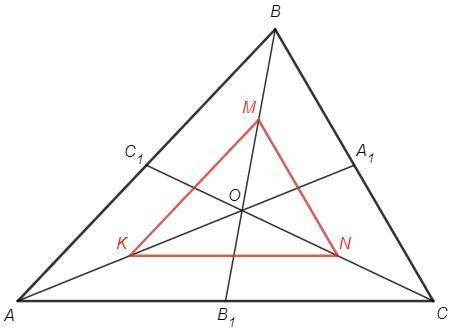
Средняя линия треугольника соединяет середины двух сторон, параллельна третьей стороне и равна ее половине.
Отрезки KM, MN, KN являются средними линиями в треугольниках AOB, BOC, AOC.
a) KM||AB, MN||BC, KN||AC
KMN~ABC по трем параллельным сторонам
б) KM=AB/2, MN=BC/2, KN=AC/2
P(ABC) =2P(KMN) =44*2 =88 (см)
в) Отношение соответствующих отрезков (медиан, биссектрис, высот и любых отрезков, построенных сходным образом) в подобных треугольниках равно коэффициенту подобия.
k=AB/KM =2
Медианы ABC вдвое больше медиан KMN.
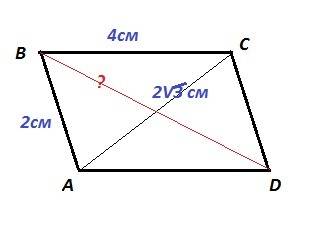
ABCD - параллелограмм. AB = 2 см, BC = 4 см, AC = 2√3 см
По теореме косинусов диагонали параллелограмма
AC² = AB² + BC² - 2 AB · BC · cos ∠B
BD² = AB² + AD² - 2 AB · AD · cos ∠A =
= AB² + AD² - 2 AB · AD · cos (180° - ∠B) =
= AB² + AD² + 2 AB · AD · cos ∠B
Так как AD = BC ⇒
BD² = AB² + BC² + 2 AB · BC · cos ∠B
Складываем почленно квадраты диагоналей.
AC² + BD² = AB² + AB² + BC² + BC²
BD² = 2 AB² + 2 BC² - AC² = 2·2² + 2·4² - (2√3)² =
= 8 + 32 - 12 = 28
BD = √28 = 2√7 см
ответ : BD = 2√7 см
вот вот вот вот вот вот
вот вот вот вот вот вот