Пусть внешний угол при вершине A равен α. Тогда угол BCD = α, а угол BAD равен 180°-α. Заметим, что сумма противоположных углов равна 180°-α+α = 180°; Значит данный четырехугольник можно вписать в окружность. Пусть ее радиус равен R; По теореме синусов: и , поскольку AD = CD, то углы ABD и DBC равны, а значит, BD - биссектриса
Для этого надо составить уравнения сторон в виде у = кх + в. У параллельных прямых коэффициенты "к" равны. Сторона АВ: Уравнение прямой: Будем искать уравнение в виде y = k · x + b . В этом уравнении: k - угловой коэффициент прямой (k = tg(φ), φ - угол, который образует данная прямая с положительным направлением оси OX); b - y-координата точки (0; b), в которой искомая прямая пересекает ось OY. k = (yB - yA) / (xB - xA) = (2 - (-6)) / (4 - (2)) = 4; b = yB - k · xB = 2 - (4) · (4) = yA - k · xA = -6 - (4) · (2) = -14 . Искомое уравнение: y = 4 · x - 14 .
Сторона ВС: k = (yB - yA) / (xB - xA) = (5 - (2)) / (-2 - (4)) = -0.5; b = yB - k · xB = 5 - (-0.5) · (-2) = yA - k · xA = 2 - (-0.5) · (4) = 4 . Искомое уравнение: y = -0.5 · x + 4 .
Сторона СД: k = (yB - yA) / (xB - xA) = (1 - (5)) / (-3 - (-2)) = 4; b = yB - k · xB = 1 - (4) · (-3) = yA - k · xA = 5 - (4) · (-2) = 13 . Искомое уравнение: y = 4 · x + 13 .
Сторона АД: k = (yB - yA) / (xB - xA) = (1 - (-6)) / (-3 - (2)) = -1.4; b = yB - k · xB = 1 - (-1.4) · (-3) = yA - k · xA = -6 - (-1.4) · (2) = -3.2 . Искомое уравнение: y = -1.4 · x - 3.2 .
Уравнения сторон АВ и СД имеют одинаковые коэффициенты "к", поэтому заданный четырёхугольник - трапеция.
См. рисунок. АЕ=СЕ => ЕР- высота , медиана и биссектриса для равнобедр. треуг. АЕС т.е. угол АРЕ=90. АР=РС и АС=2АВ => AB=AP => треуг. BAP равнобедр. => биссектриса АЕ - высота и медиана, т.е. ВО=ОР и все углы при т.О=90 теперь, треугольники ВОЕ и РОЕ равны по сторонам ВО=ОР, ОЕ- общая и угол между ними =90,отсюда ВЕ=РЕ, отсюда треугольники АВЕ и АРЕ равны. Но т.к. угол АРЕ=90 (см. выше), тогда и АВЕ=90. Все, нашли.
Но тут можно продолжить изыскания. Мы имеем прямоугольный треугольник, у которого один катет АВ в два раза меньше гипотенузы АС. Значит, он лежит против угла в 30 градусов. Значит, наш треугольник имеет углы в 30,60 и 90 градусов.
Пусть внешний угол при вершине A равен α. Тогда угол BCD = α, а угол BAD равен 180°-α. Заметим, что сумма противоположных углов равна 180°-α+α = 180°; Значит данный четырехугольник можно вписать в окружность. Пусть ее радиус равен R; По теореме синусов: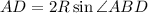
и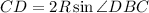 
, поскольку AD = CD, то углы ABD и DBC равны, а значит, BD - биссектриса