1. По Пифагору квадрат второго катета равен 36²-12²=(36-12)*(36+12)=24*48
И этот же квадрат катета равен произведению гипотенузы на искомую проекцию этого катета на гипотенузу, поэтому проекция равна 48*24/36=8*24/6=8*4=32/см/
2. Площадь треугольника АВС равна половине произведения АВ и АС на синус 45°, т.е. 5√2*8*(√2/2)/2=20
средними линиями мы разбиваем треугольник на четыре равных, а значит, и равновеликих, т.е. с равными площадями. поэтому искомая площадь 20/4=5/см²/
4. формулы параллельного переноса
х'=x+a
y'=y+b
0=3+a⇒a=-3
6=2+b⇒b=4
Пусть С(х;у)
х+а=-3
у+b=2, подставим а и b для точек С и D, получим
х+(-3)=-3⇒х=0
у=-4+2=-2
D(0; -2)
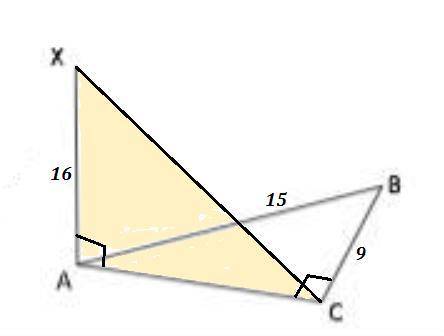
ΔABC - прямоугольный , ∠С=90° , ХА ⊥ АВС ⇒ ХА⊥АС .
а) Если провести отрезок ХС , то он будет перпендикулярен катету ВС , так как по теореме о трёх перпендикулярах , если АС⊥ВС и АС - проекция наклонной ХС на плоскость АВС , то и сама наклонная ХС будет перпендикулярна катету ВС , ХС ⊥ ВС .
б) ХА=16 , АВ=15 , ВС=9
Расстояние от точки до прямой - это длина перпендикуляра, опущенного из этой точки на прямую.
Поэтому длина ХС - это и есть расстояние от точки Х до прямой ВС .
По теореме Пифагора : АС²+ВС²=АВ² ⇒ АС²=АВ²-ВС²=15²-9²=144 .
Рассм. ΔХАС . Он прямоугольный, так как ХА ⊥ АС .
По теореме Пифагора : ХА²+АС²=ХС² ⇒ ХС²=16²+144=400 ,
ХС=20 см .
пусть на сторону с длиной а падает высота с длиной Ha=8,
а на сторону с длиной b падает высота с длиной Hb=4,
тогда S=Hb*b=Ha*a
P=2*(a+b)=30, a+b=15
2S=Hb*b+Ha*a=4b+8a=4b+4a+4a=4(b+a)+4a=4*15+4a=60+4a
2S=60+4a
S=30+2a
при этом S=Ha*a=8*a
значит 30+2a=8a
6a=30
a=5
S=Ha*a=8*5=40
ответ:40