Высота конуса, образующая и половина диаметра образуют прямоугольный треугольник с углами 30 и 60 градусов. По свойству данного треугольника: катет лежащий против угла 30 градусов в два раза меньше гипотенузы.
Высота h - катет лежащий против угла 30 градусов;
Образующая равна 2h;
По т. Пифагора: 9²+h²=(2h)² ⇒
h=3√3 - высота конуса;
2h=6√3 - образующая конуса.
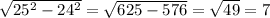
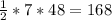
при ВС ∥АД и секущей СО
Но угол ВСО=углу ОСД по условию.
Значит, в треугольнике СОД угол СОД=углу ОСД и треугольник ОСД - равнобедренный
ОД=СД=17
2 Угол ВОА=углу ОВС как накрест лежащие при ВС ∥АД и секущей ВО
Но угол ОВС = углу АВО по условию
Значит, в треугольнике АВО углы при основании равны и он - равнобедренный.
АВ=АО=10
3. АД= АО+ОД=10+17=27
4. В прямоугольном треугольнике АВК найдем АК по теореме Пифагора.
АК =корень из ( 10^2-8^2)=6
5. В прямоуг. треугольнике МСД найдем МД по теореме Пифагора
МД = корень из ( 17^2-8^2)=15
6.ВС= АД-АК-МД=27-6-15=6
7.Ищем площадь классически - полусумма оснований на высоту. S авсд= (6+27 *8)/2=132
Проведём высоту к основанию конуса, и рассмотрим его осевое сечение - это р / б треугольник: диаметр основания это основание,а две образующие ,выходящие из концов данного диаметра - боковые стороны.
Высота конуса совпадает с высотой р/б треугольника , и делит его на два равных прямоугольных треугольника.
Рассмотрим один из них:
Один из катетов равен половине диаметра(радиусу) основания цилиндра 9см.
Гипотенуза это образующая конуса.
Угол между катетом в 9см и гипотенузой равен 30*.
Второй катет совпадает с высотой р/б треугольника(конуса).
Косинус — есть отношение прилежащего катета к гипотенузе.
Синус — есть отношение противолежащего катета к гипотенузе
Найдём гипотенузу через косинус:
Найдём высоту через синус