Предлагаю то же самое решение, как и у уважаемого valenivan, только "в профиль"
Как известно, (а кому не известно, то доказывается в 6 секунд, например, у valenivan в началных строчках), что высота такого треугольника равна сумме указанных расстояний, т.е. h=1/7+2.8+1.5=6
но h=a√3/2=6 ⇒a=12/√3
высота есть, сторона тоже, площадь находится элементарно
S=12√3
В равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его медианы. Тогда треугольники AKB и ALB равны по второму признаку равенства треугольников. У них сторона AB общая, стороны AL и BK равны как половины боковых сторон равнобедренного треугольника, а углы LAB и KBA равны как углы при основании равнобедренного треугольника. Так как треугольники равны, их стороны AK и LB равны. Но AK и LB - медианы равнобедренного треугольника, проведённые к его боковым сторонам.
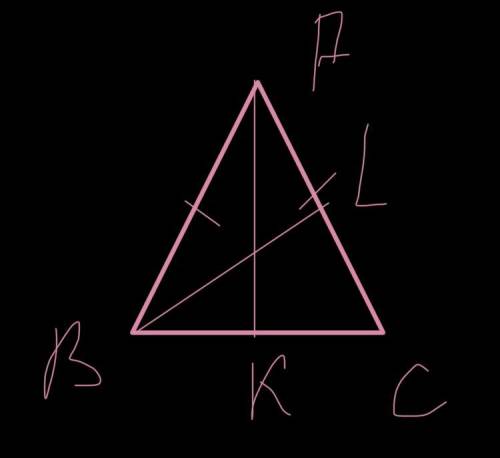
В равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его медианы. Тогда треугольники AKB и ALB равны по второму признаку равенства треугольников. У них сторона AB общая, стороны AL и BK равны как половины боковых сторон равнобедренного треугольника, а углы LAB и KBA равны как углы при основании равнобедренного треугольника. Так как треугольники равны, их стороны AK и LB равны. Но AK и LB - медианы равнобедренного треугольника, проведённые к его боковым сторонам.
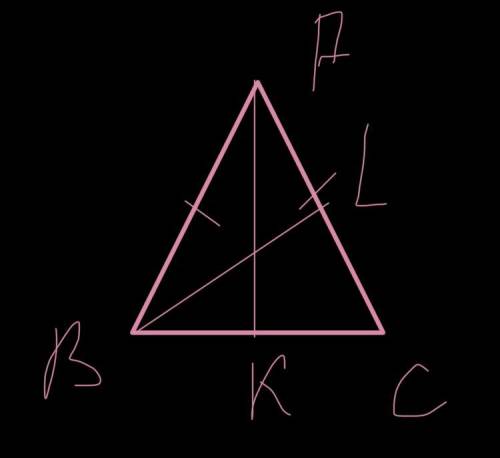
Решение задания приложено