ответ: Коллинеарны.
Объяснение:
Что бы векторы были коллинеарны, достаточно, что бы координаты одного вектора получались умножением координат второго на одно и то же число, то есть, к примеру, вектор а=m*b
Пусть это число m. Тогда
для координат у имеем 1*m= 2 и отсюда сразу m=2
Теперь составим два уравнения для координат х и z
для координат х
имеем 2*m = n², то есть 2*2 = n², а отсюда n=2 или n=-2
Для координат z
имеем n*m = -4, то есть 2n = -4, отсюда n= -2
Значит n=2 не годится, и остается n = -2
проверим, для чего координаты вектора а должны получаться при умножении координат вектора b на m, то есть на 2. При этом n=-2 :
2*2= (-2)² - верно
1*2=2 - верно
-2*2= -4 - верно.
Векторы коллинеарны.
35113996
* * * * * * * * * * * * * * * * * * *
Без лишних слов ( эмоции )
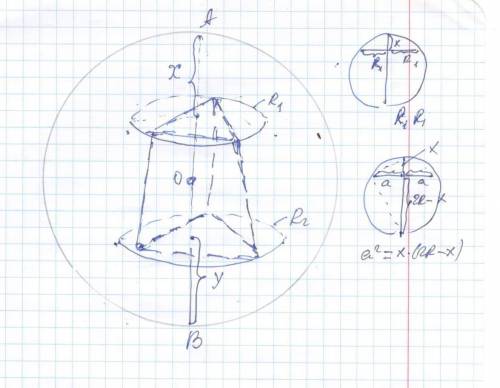
R₁ =3√3* √3 /3 = 3 * * * R =(a√3/2)*2/3 =(a√3)/3 * * *
R₂ =4√3* √3 /3 = 4
R₁² = x (2R - x) ⇔x² - 2Rx + 9 = 0 ⇒ x₁ =R -√(R²- 9)
Маленький кусок диаметра x₁ =12 (между основания со стороной 3√3 и поверхностью шара) ( большой кусок x₂=R+ -√(R²- 9) )
Аналогично
R₂² = y (2R -y) ⇔ y² - 2Ry + 16=0 ⇒ y ₁ = R -√(R²- 16 )
x₁+ H + y₁ = 2R ⇔ R -√(R²- 9) + 7 + R -√(R²- 16) = 2R ⇔
R -√(R²- 9) + 7 + R -√(R²- 16) =2R ;
√(R²- 9) + √(R²- 16) =7 * * * ясно R =5 * * *
для сомневающихся (неужели нет другое решение ?)
примитивное иррациональное уравнение
необязательная замена t =R² > 0
√(t- 16) = 7 -√(t - 9) ⇔ t- 16 =49 -14√(t - 9) + t -9⇔ 14√(t - 9) =56 ⇔
t - 9 = 4² ⇔ t =25
R² =25 ⇒ R = 5 ( R = -5 построенное решение )
ответ : 5 см .
Изменение
добавил неповторимый пейзаж
Тупоугольный треугольник АВС
Угол А тупой
Сторона ВС = 4
Медианы АЕ, BF, CD
Координаты вершин
A(x;y)
B(2;0)
C(-2;0)
D((2+x)/2;y/2)
E(0;0)
F((x-2)/2;y/2)
Тупоугольным треугольник будет только если вершина А лежит внутри окружности, построенной на стороне CD и диаметром 4
AE² = x² + y² < 2²
|AE| < 2
Медиана АЕ меньше 2
Медиана ВF
ВF² = (2 – (x-2)/2)² + y²/4 = 1/4*(x² – 12x + y² + 36)
Медиана СD
CD² = ((2+x)/2+2)² + y²/4 = 1/4*(x² + 12x + y² + 36)
Сумма медиан CD и BF
S(x;y) = 1/2*sqrt(x² – 12x + y² + 36) + 1/2*sqrt(x² + 12x + y² + 36)
Производная по x, ищем экстремум
dS/dx = 1/4*((2(x - 6))/sqrt(x² - 12x + y² + 36) + (2(x + 6))/sqrt(x² + 12x + y² + 36)) = 0
(x - 6)/sqrt(x² - 12x + y² + 36) + (x + 6)/sqrt(x² + 12x + y² + 36) = 0
Числитель
(x - 6)*sqrt(x² + 12x + y² + 36) + (x + 6)*sqrt(x² - 12x + y² + 36) = 0
Тривиальное решение
х = 0 для любого y
Знаменатель при этом неважен, лишь бы оставался ненулевым
Это экстремум, но минимум или максимум — пока неизвестно.
Для определения проще всего вычислить значение S(0;2) и S(1;2)
S(0;2) = 1/2*sqrt(4 + 36) + 1/2*sqrt(4 + 36) = sqrt(40) ≈ 6,325
S(1;2) = 1/2*sqrt(1 – 12 + 4 + 36) + 1/2*sqrt(1 + 12 + 4 + 36) = 1/2*sqrt(29) + 1/2*sqrt(53) ≈ 6,333
Т.е. при x = 0 имеется минимум суммы длин медиан
Минимальной суммой медиан к боковым сторонам обладает равнобедренный треугольник
Производную по y можно не брать, т. к. по y сумма длин — функция возрастающая и максимальное значение суммы длин будет при максимальном значении y
Но из условия тупоугольности треугольника у нас y не может превосходить 2
Медиана к основанию тоже не превосходит 2, поэтому значение сумм длин всех трёх медиан будет не превосходить
S(0;2) + 2 = 2 + sqrt(40) ≈ 8,325
Что меньше требуемых по условию 9