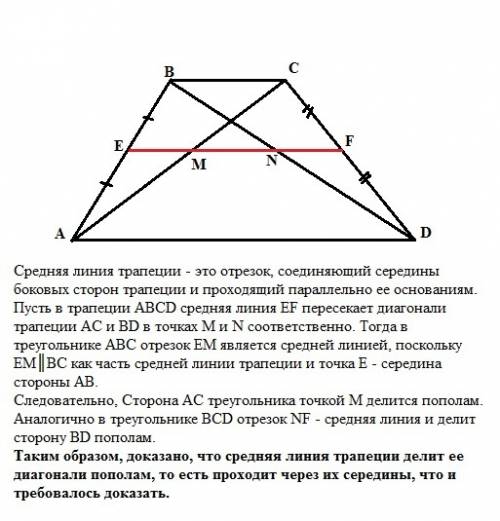
Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон трапеции и проходящий параллельно ее основаниям.
Пусть в трапеции АВСD средняя линия EF пересекает диагонали трапеции АС и ВD в точках М и N соответственно. Тогда в треугольнике АВС отрезок ЕМ является средней линией, поскольку ЕМ║ВС как часть средней линии трапеции и точка Е - середина стороны АВ.
Следовательно, Сторона АС треугольника точкой М делится пополам.
Аналогично в треугольнике ВCD отрезок NF - средняя линия и делит сторону BD пополам.
Таким образом, доказано, что средняя линия трапеции делит ее диагонали пополам, то есть проходит через их середины, что и требовалось доказать.
Дано: ABCD, AB║CD, BC ║AD, AB = √13, BC = 6, ∠A = 60 °, S=?
S = a*h, a = BC = 6, h = BK, BK⊥AD
ΔABK - прямоугольный. ∠А = 60°, ∠В = 30° , ⇒AК = √13/2
по т. Пифагора ВК² = 13² - (√13/2)² = 169 - 169/4 = 169*3/4
ВК = h = 13√3/2
S = 6*13√3/2 = 39√3
S = 39√3