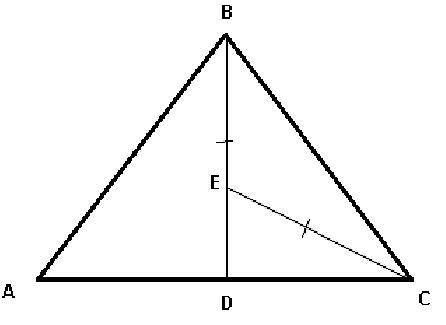
Пусть точка Е лежит на медиане BD равнобедренного треугольника
ED = 14 см и CE = 50 см. Поскольку отрезки от концов боковой
стороны равноудалены, то BE = CE = 50 см. Из прямоугольного
треугольника EDC по теореме Пифагора:
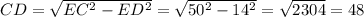 см
см
Поскольку BD - медиана равнобедренного треугольника, то
она является и высотой и биссектрисой. Тогда BD = 14+50 = 64 см.
По теореме Пифагора из прямоугольного треугольника BDC:
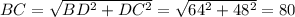 см.
см.
AC = 2 * DC = 2 * 48 = 96 см. Тогда периметр треугольника равен
P = AB + BC + AC = 80 + 80 + 96 = 256 см
Длина окружности равна: C = 2πR откуда R = C/2π = 72π/2π = 36 см. На рисунке OK = R = 36 см и ОК ⊥ СВ.
Пусть коэффициент пропорциональности равен х, тогда KC=9x, BK = 4x.
ОК является высотой прямоугольного треугольника BOC, тогда, используя свойства пропорциональные отрезки в прямоугольном треугольнике, получим
Сторона ромба: BC = KC + BK = 9x + 4x = 13x = 13*6=78 см. Если радиус ОК продолжить к стороне АD и обозначим точку касания L, то LK - диаметр окружности и является высотой ромба.
ответ: 5616 см².