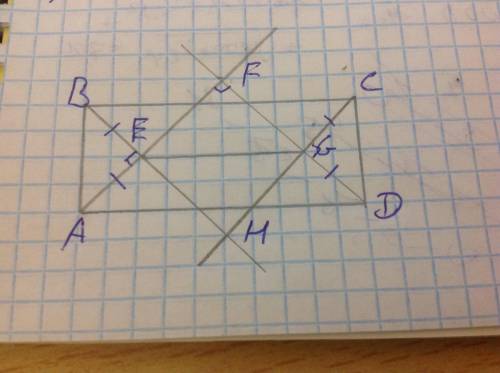
Пусть в прямоугольнике ABCD биссектрисы пересекаются в точках E,F,G,H. Докажем, что EFGH - квадрат. В треугольнике AFD углы A и D равны 45 градусам, тогда угол F равен 90 градусам. Аналогично, в треугольнике BCH углы B и C равны 45 градусам, а угол H равен 90 градусам. В треугольнике ABE углы A и B равны 45 градусам, тогда угол E равен 90 градусам. Тогда и угол FEH равен 90 градусам (вертикальные углы равны). Аналогично, в треугольнике CDG углы C и D равны 45 градусам, тогда угол G равен 90 градусам и угол FGH равен 90 градусам. Таким образом, все углы четырехугольника EFGH равны 90 градусам и этот четырехугольник является прямоугольником.
Теперь докажем, что соседние стороны EF и FG этого прямоугольника равны. Треугольники ABE и CDG равны, так как каждый из них - равнобедренный и прямоугольный и их гипотенузы равны. Тогда AE=DG. Треугольник ADF является равнобедренным и прямоугольным, тогда AF=DF. Тогда EF=AF-AE, GF=DF-DG, откуда EF=GF, треугольник EFG равнобедренный и EF=FG. Так как в прямоугольнике EFGH соседние стороны равны, этот прямоугольник - квадрат, что и требовалось доказать.
Объяснение:
Площадь треугольника: S=(1/2)*a*b*Sinα. Sinα = Sin(180°-α) (тригонометрия). Угол α - угол между диагоналями. Отсюда:
Sbco=(1/2)*BO*OC*Sinα (1).
Saod=(1/2)*AO*OD*Sinα (2).
Saob=(1/2)*AO*OB*Sinα (3).
Sdoc=(1/2)*OC*OD*Sinα (2). Отсюда
Sbco*Saod=Saob*Sdoc=(1/4)*BO*OA*DO*OC*Sin²α = 1*9 = 9.
Но Sabo+Scod =Sabcd - Sbco - Saod =16-10=6 см². =>
Решая систему двух уравнений: Sabo+Scod=6 и Sabo*Scod =9 Получим Sabo = Scod =3 см².