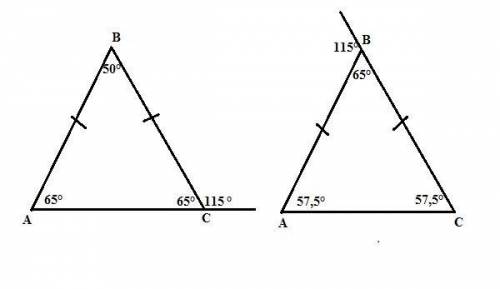
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
Дано: Треугольник АВС. АВ=ВСб М∈BD, K∈AC. MK║AB. <ABC=126°,<BAC=27°.
Найти <MKD, <KMD и <MDK.
Решение.
Треугольник АВС равнобедренный, следовательно BD - биссектриса, высота и медиана треугольника. <BAC=<BCA=27°, Значит
<ABD = (1/2)*(<ABC) = 126/2 = 63°. <BDA=<MDK = 90°.
MK параллельна АВ, значит <MKD=<BAC=27°, а <KMD=<ABD=63°, как соответственные углы при параллельных прямых АВ и МК и секущих AD и BD соответственно.
ответ: <MKD=27°, <KMD=63°, <MDK=90°.

Пусть
Дано:
АВСД р/б трапеция
Р (АВСД = 42 см
ВС - меньшее осн = 3 см
АС - биссектр уг ВСД
ВН - высота
ВН - ?
1) Т к по усл АС - бисс уг ВСД, то уг ВСА = уг ДСА,
2) уг ВСА и уг САД являются внутренними накрест лежащими при ВС||AD и секущей АС, значит уг ВСА = уг САД и = уг АСД, а значит тр АСД - р/б с основанием АС по признаку р/б треугольника.
3) т к по усл АВСД - трап - р/б , то СА = СД и = АС из п2
4) Р(АВСД) = 42 см
Р(АВСД) = АВ + ВС + СД + ДА = ВС + 3 АВ
42 = 3 + 3 АВ
39 = 3 АВ
АВ = 13 (см) = ВД = ДА
5) Т к трапеция АВСД - р/б , то АД = 2АН + ВС => AH = (13 - 3 ) : 2 = 5 см
6) Рассм тр АВН ( уг Н = 90*, по условию ВН - высота)
АВ² = ВН²+АН²
ВН² = 169 - 25
ВН² = 144
ВН = 12 см -искомая высота трапеции