Основание пирамиды - ромб с большей диагональю d и острым углом альфа. все двугранные углы при основании пирамиды равны бета. найдите площадь боковой поверхности пирамиды.
Пусть AC - большая диагональ ромба; AC = d и острый угол . Диагонали ромба являются биссектрисами его углов, пересекаются под прямым углом и в точке пересечения делятся пополам.
Из прямоугольного треугольника AOD: отсюда выразим AD:
Площадь ромба равна S = a*h, с другой стороны: S = a²*sinα, приравнивая площади, получим h = a * sin α, где а - сторона ромба.
- высота ромба.
Высота ромба является диаметром вписанной окружности в ромб, тогда радиус вписанной окружности равен
Рассмотрим теперь прямоугольный треугольник SOK и найдем в нем SK - апофему пирамиды:
Найдем теперь площадь боковой поверхности пирамиды
Любая вписанная трапеция равнобокая, так как углы, опирающиеся на одну дугу, должны быть равны. Обозначим основания трапеции за 2x и 2y. Тогда средняя линия равна (2x + 2y)/2 = (x + y),
Уравнения:
Решаем первое уравнение.
Подставляя во второе уравнение и немного мучаясь, можно получить ответ x = 6, y = 8.
Уравнения будут выглядеть немного лучше, если обозначить куски высоты как 4x и 3x. Тогда уравнение будет выглядеть следующим образом: Получающееся квадратное уравнение радует количеством вычислений.
Наконец, можно обозначить неизвестными углы H1CO = x и H2DO = y Тогда система получится простой: Но решать её всё равно неинтересно.
P = 2x + y (x - боковые стороны, y - основание) y = 96, P = 196 - дано в условии, найдем x 2X=P-y x= (P-y)/2 x=50
итого: x = 50, y = 96 нам не хватает высоты, для нахождения площади. Проведем высоту и рассмотрим половинку этого равнобедренного треугольника, где гипотенуза - x, а прилежащий катет - y/2 (т.к высота в равнобедренном треугольника - медиана) по теореме Пифагора h = √(x^2 - (y/2)^2) h = √(50^2 - 48^2) = √196 = 14
Площадь треугольника: половина основания на высоту, основание - y, высота - h тогда: S=1/2*hy = 96*14/2 = 672. ответ: 672
Пусть AC - большая диагональ ромба; AC = d и острый угол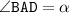 . Диагонали ромба являются биссектрисами его углов, пересекаются под прямым углом и в точке пересечения делятся пополам.
. Диагонали ромба являются биссектрисами его углов, пересекаются под прямым углом и в точке пересечения делятся пополам.
Из прямоугольного треугольника AOD: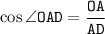 отсюда выразим AD:
отсюда выразим AD: 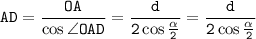
Площадь ромба равна S = a*h, с другой стороны: S = a²*sinα, приравнивая площади, получим h = a * sin α, где а - сторона ромба.
Высота ромба является диаметром вписанной окружности в ромб, тогда радиус вписанной окружности равен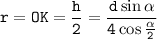
Рассмотрим теперь прямоугольный треугольник SOK и найдем в нем SK - апофему пирамиды: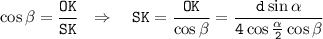
Найдем теперь площадь боковой поверхности пирамиды