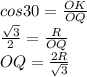
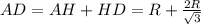
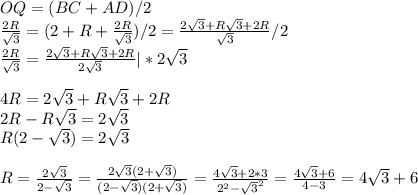
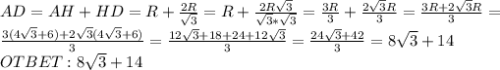
См. Объяснение
Объяснение:
Задача 1
Найдите площадь трапеции,
у которой средняя линия равна 10 см, боковая сторона 6 см и составляет с одним из оснований угол 30°.
Решение
1) Находим высоту трапеции. Она равна произведению боковой стороны на синус углу 30°:
h = 6 · sin 30° = 6 · 0,5 = 3 см
2) Площадь трапеции равна произведению средней линии на высоту:
S = 10 · 3 = 30 cм²
ответ: 30 cм²
Задача 2
Диагонали выпуклого четырехугольника равны 3 см и 4 см. Какую наибольшую площадь может иметь этот четырехугольник?
Решение
Максимальной площадь четырёхугольника будет тогда, когда диагонали будут пересекаться под углом 90°.
Это следует из того, что при пересечении диагоналей образуется 4 треугольника, площадь каждого из которых рассчитывается как половина произведения сторон на синус угла между ними, а так как максимальное значение синуса угла равно 1, то это значит что угол между диагоналями должен быть 90°.
Пусть диагонали делятся в точке пересечения на отрезки:
х и (3-х),
у и (4-у).
Тогда площади полученных 4-х прямоугольных треугольников, образованных пересечением диагоналей, будут соответственно равны:
S₁= ху/2,
S₂=(3-х)у/2
S₃=(4-у)(3-х)/2
S₄=(4-у)х/2
Сложив эти площади, получим:
S = S₁+S₂+S₃+S₄ = (ху+3у-ху+12-4х-3у+ху+4х-ху):2 = 12:2 = 6 см²
Следовательно, наибольшая площадь S выпуклого четырёхугольника с диагоналями 3 см и 4 см равна 6 см².
ответ: 6 см².
Алан Метисон Тьюринг; 23 июня 1912 — 7 июня 1954) — английский математик, логик, криптограф, оказавший существенное влияние на развитие информатики. Кавалер Ордена Британской империи (1945), член Лондонского королевского общества (1951)[5]. Предложенная им в 1936 году абстрактная вычислительная «Машина Тьюринга», которую можно считать моделью компьютера общего назначения, позволила формализовать понятие алгоритма и до сих пор используется во множестве теоретических и практических исследований. Научные труды А. Тьюринга — общепризнанный вклад в основания информатики (и, в частности, — теории искусственного интеллекта)[7].
Во время Второй мировой войны Алан Тьюринг работал в Правительственной школе кодов и шифров, располагавшейся в Блетчли-парке, где была сосредоточена работа по взлому шифров и кодов стран оси. Он возглавлял группу 8, ответственную за криптоанализ сообщений военно-морского флота Германии. Тьюринг разработал ряд методов взлома, в том числе теоретическую базу для Bombe — машины, использованной для взлома немецкого шифратора Enigma.
После войны Тьюринг работал в Национальной физической лаборатории, где по его проекту был реализован первый в мире компьютер с хранимой в памяти программой — ACE. В 1948 учёный присоединился к вычислительной лаборатории Макса Ньюмана в Университете Манчестера, где ассистировал при создании Манчестерских Компьютеров[8], а позднее заинтересовался математической биологией. Тьюринг опубликовал работу по химическим основам морфогенеза и предсказал протекающие в колебательном режиме химические реакции, такие, как реакция Белоусова — Жаботинского, которые впервые были представлены научному сообществу в 1968 году. В 1950 году предложил эмпирический тест Тьюринга для оценки искусственного интеллекта компьютера.
В честь учёного названа Премия Тьюринга — самая престижная в мире награда в области информатики.